¿Qué es una Función de Densidad de Probabilidad?

Entendiendo los Conceptos Básicos de las Funciones de Densidad de Probabilidad

¿Por Qué Necesitamos las FDP?

Las funciones de densidad de probabilidad (FDP) son herramientas vitales en el análisis probabilístico, ya que nos permiten representar el comportamiento de variables aleatorias continuas. Mientras que las variables aleatorias discretas usan funciones de masa de probabilidad (FMP) para asignar probabilidades en puntos específicos, las variables aleatorias continuas no pueden tener probabilidades no nulas en ubicaciones específicas, y por lo tanto, las probabilidades deben distribuirse en intervalos - este proceso de distribución es algo que describen las FDP asignando densidades probabilísticas en cada posible valor.

Considere medir la altura entre personas en una población. La altura es una variable continua - sus valores oscilan entre 160.4 cm y 164.425 cm - creando así la necesidad de usar funciones de densidad de probabilidad para describir ciertos rangos. Una FDP podría decirnos, por ejemplo, que los individuos alrededor de 170 cm tienen mayores probabilidades en comparación con 180 cm, aunque mediciones exactas como 171.038 cm no tengan probabilidades exactas.

Las distribuciones discretas, como lanzar un dado justo de seis caras, operan de manera diferente. En este caso, los resultados individuales tienen probabilidades distintas (e.g., \(P(X = 3) = \frac{1}{6}\)). Las FDP generalizan los cálculos de probabilidad a intervalos para variables continuas, haciéndolas invaluables en campos como estadística, finanzas y análisis de datos científicos.

Definiciones Clave de las FDP

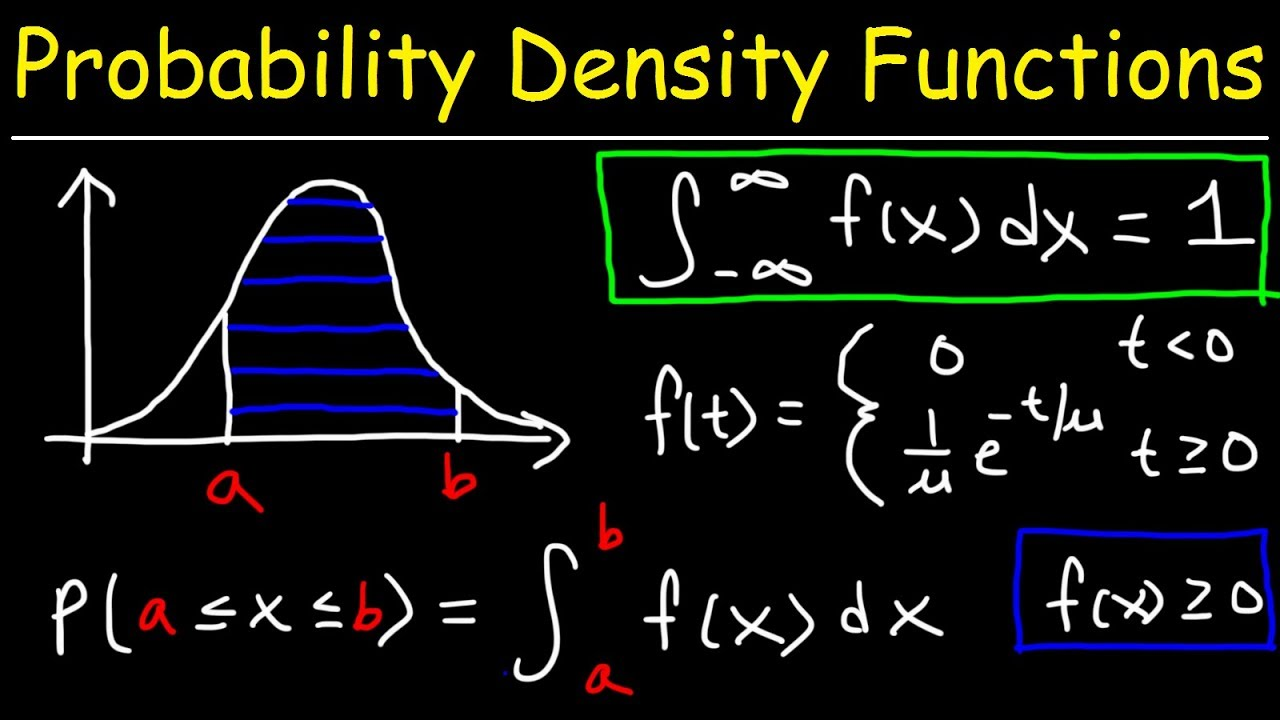
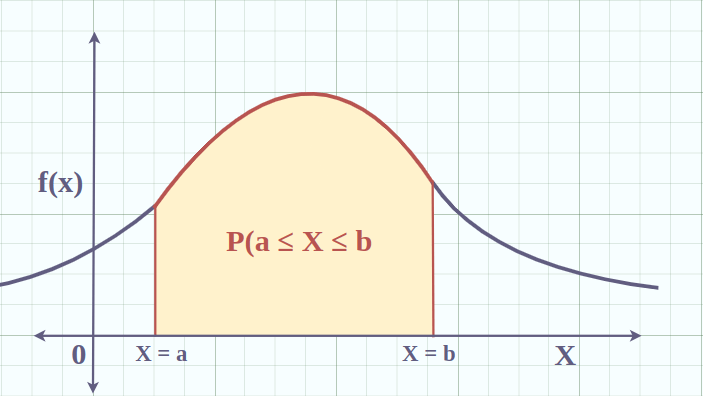
Una función de densidad de probabilidad representa la probabilidad por unidad de longitud. Para una variable aleatoria \(X\), su FDP \(f_X(x)\) proporciona una manera de calcular probabilidades sobre intervalos. La probabilidad de que \(X\) caiga dentro de un intervalo \([a, b]\) se da por:

\(P(a \leq X \leq b) = \int_a^b f_X(x) dx\)

El valor de \(f_X(x)\) en un punto \(x\) en sí mismo no representa probabilidad sino más bien la densidad de probabilidad alrededor de \(x\). Matemáticamente, se define como el límite de la razón:

\(f_X(x) = \lim_{\Delta \to 0+} \frac{P(x < X \leq x + \Delta)}{\Delta}\)

Así, las FDP son fundamentales para describir cómo se distribuyen las probabilidades para las variables continuas.

Las FDP y Analogías en la Vida Real

Las FDP pueden ser más fáciles de comprender si se ven como similares a la densidad de masa en física; así como la masa se distribuye sobre un área (por ejemplo, gramos por centímetro), distribución de probabilidad ocurre a través de valores en variables aleatorias. Si la densidad en un cierto punto en una curva de distribución de masa es alta, esto indica que mucha masa existe en esa región. De la misma manera, un valor alto de una FDP indica una alta concentración de probabilidad en un rango específico. La masa total corresponde a una probabilidad total de 1, correspondiendo al requerimiento fundamental de una FDP.

Los Fundamentos Matemáticos de las PDFs

La Definición Formal de una PDF

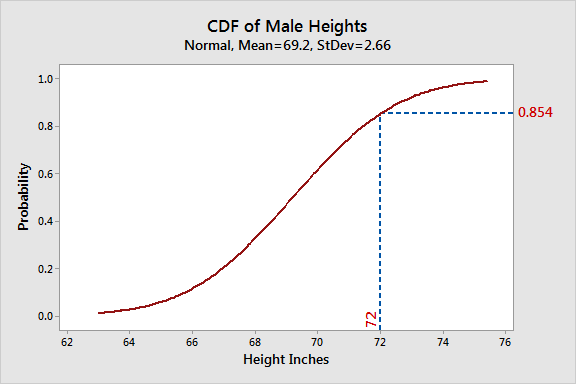
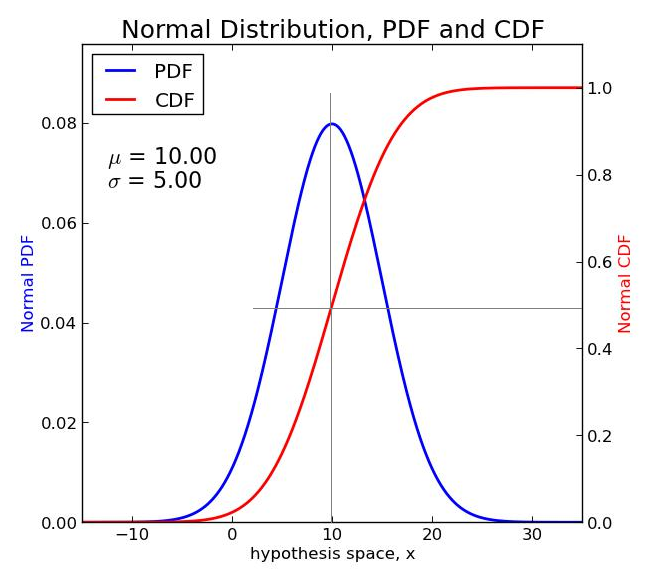
Una función de densidad de probabilidad se define formalmente en relación con la función de distribución acumulativa (CDF) de una variable aleatoria \(X\). La CDF \(F_X(x)\) proporciona la probabilidad de que \(X\) sea menor o igual a \(x\), y la PDF se deriva como la derivada de la CDF:

\(f_X(x) = \frac{dF_X(x)}{dx}\)

Asimismo, la CDF puede obtenerse integrando la PDF:

\(F_X(x) = \int_{-\infty}^x f_X(u) du\)

Esta relación entre una PDF y una CDF es crucial para comprender cómo se distribuyen las probabilidades. Por ejemplo, si sumas todas las probabilidades hasta un cierto valor \(x\), la CDF captura esta probabilidad acumulada, mientras que la PDF representa la tasa de cambio en ese punto.

Propiedades de las PDFs

Propiedades Fundamentales

1. No Negatividad: La PDF \(f_X(x)\) es siempre mayor o igual a 0 para todos los valores de \(x\):

\(f_X(x) \geq 0\)

Esto asegura que las probabilidades o densidades no pueden ser negativas.

2. Normalización: El área bajo toda la curva de la PDF es igual a 1:

\(\int_{-\infty}^{+\infty} f_X(x) dx = 1\)

Esta propiedad garantiza que la probabilidad total sobre todos los valores posibles de \(X\) es igual a 1, reflejando los principios fundamentales de la teoría de la probabilidad.

3. Interpretación de Probabilidad para Intervalos: La probabilidad de que \(X\) caiga dentro de un intervalo \([a, b]\) se da por:

\(P(a \leq X \leq b) = \int_a^b f_X(x) dx\)

Esto permite que las PDFs se utilicen para cálculos prácticos de probabilidad.

Soporte y Restricciones

Una PDF se define sobre el soporte de una variable aleatoria, que es el conjunto de todos los valores posibles donde \(f_X(x) > 0\). Por ejemplo, si una variable solo toma valores positivos, su PDF podría tener un soporte de \([0, \infty)\).

Entendiendo las Propiedades de las PDF con Ejemplos

Para ilustrar las propiedades de las PDFs, considera la distribución uniforme para \(X\) sobre \([0, 1]\). La PDF es constante, \(f_X(x) = 1\), a lo largo de este intervalo. No hay probabilidad fuera de este rango porque \(f_X(x) = 0\) de otro modo. Calcular el área total bajo esta curva confirma que integra a 1:

\(\int_0^1 1 \, dx = 1\)

De manera similar, computar \(P(0.2 \leq X \leq 0.8)\) requiere una integral sobre el intervalo:

\(P(0.2 \leq X \leq 0.8) = \int_{0.2}^{0.8} 1 \, dx = 0.8 - 0.2 = 0.6\)

Estos cálculos resaltan directamente cómo las propiedades fundamentales de las PDFs se aplican en la práctica.

La Relación entre PDFs y CDFs

De CDF a PDF

La relación entre las funciones de densidad de probabilidad (PDFs) y las funciones de distribución acumulativa (CDFs) refleja la estructura matemática más profunda de la probabilidad. Una CDF \(F_X(x)\) caracteriza la probabilidad de que la variable aleatoria \(X\) tome un valor menor o igual a \(x\):

\(F_X(x) = P(X \leq x)\)

Derivar la PDF de la CDF implica la diferenciación:

\(f_X(x) = \frac{dF_X(x)}{dx}\)

Por ejemplo, considere una variable aleatoria uniforme \(X\) sobre \([0, 1]\) con la CDF:

\(F_X(x) = \begin{cases} 0, & x < 0 \\ x, & 0 \leq x \leq 1 \\ 1, & x > 1 \end{cases}\)

Diferenciar esto genera la PDF:

\(f_X(x) = \begin{cases} 1, & 0 \leq x \leq 1 \\ 0, & \text{en caso contrario.} \end{cases}\)

Esto representa una PDF constante sobre \([0, 1]\).

De PDF a CDF

Por el contrario, podemos reconstruir la CDF integrando la PDF:

\(F_X(x) = \int_{-\infty}^x f_X(u) du\)

Como ejemplo, tome la PDF de una distribución exponencial:

\(f_X(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases}\)

La CDF se obtiene mediante la integración:

\(F_X(x) = \begin{cases} 1 - e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases}\)

Esta relación bidireccional destaca cómo las PDFs y las CDFs se complementan en la representación de probabilidades continuas.

Interpretación de PDFs: ¿Qué Nos Dice?

El Significado de la Densidad de Probabilidad en un Punto

La interpretación de la densidad de probabilidad es fundamental para entender los PDFs. A diferencia de las funciones de probabilidad discreta que asignan probabilidades no nulas a resultados individuales, los PDFs solo describen densidades, no probabilidades absolutas, en puntos específicos. Para una variable aleatoria continua \(X\), la probabilidad de que \(X\) tome un valor exacto \(x\) es siempre cero:

\(P(X = x) = 0, \, \text{para cualquier } x\)

En cambio, el valor del PDF \(f_X(x)\) en un punto \(x\) refleja la probabilidad relativa de encontrar \(X\) cerca de ese valor. Por ejemplo, si \(f_X(x_1) > f_X(x_2)\), las áreas alrededor de \(x_1\) son más propensas a contener observaciones en comparación con \(x_2\).

Para calcular probabilidades o probabilidades relativas, se debe evaluar la probabilidad total sobre un intervalo integrando el PDF:

\(P(a \leq X \leq b) = \int_a^b f_X(x) dx\)

Por lo tanto, \(f_X(x)\) no es una probabilidad sino que mide cómo se distribuye la probabilidad a través de los valores de \(X\).

Visualizando PDFs para una Mejor Intuición

Imagina hacer un zoom en un gráfico de PDF en un punto específico \(x\) y examinar un pequeño intervalo \([x, x + \delta]\). La probabilidad aproximada de que \(X\) esté en este intervalo se puede calcular usando la función de densidad:

\(P(X \in [x, x + \delta]) \approx f_X(x) \cdot \delta\)

Por ejemplo, considera una distribución normal de los pesos de las personas. El PDF puede alcanzar su pico cerca de un peso medio como 70 kg, sugiriendo que la mayor densidad de probabilidades se concentra aquí.

Usos Generales de la Interpretación del PDF

Los PDFs ofrecen más que beneficios matemáticos; sus aplicaciones en el mundo real se extienden mucho más allá de las matemáticas puras. Por ejemplo, cuando se utilizan para asegurar el control de calidad en piezas de fabricación, los PDFs proporcionan a los ingenieros una forma de monitorear dimensiones que caen dentro de los límites de tolerancia aceptables mientras identifican eficazmente áreas con mayor probabilidad y variabilidad.

Aplicaciones Ejemplares de PDFs en Escenarios del Mundo Real

Aplicaciones en Estadística y Ciencia de Datos

Los PDFs juegan un papel integral en el análisis inferencial estadístico y la estimación de verosimilitud, incluyendo la construcción de modelos. Al ajustar distribuciones normales a datos como puntajes de exámenes, los PDFs ayudan a deducir probabilidades asociadas con valores observados bajo supuestos específicos; por ejemplo, ajustando uno, los investigadores pueden calcular cuántos estudiantes obtuvieron puntajes por encima o dentro de ciertos rangos de umbral en los exámenes.

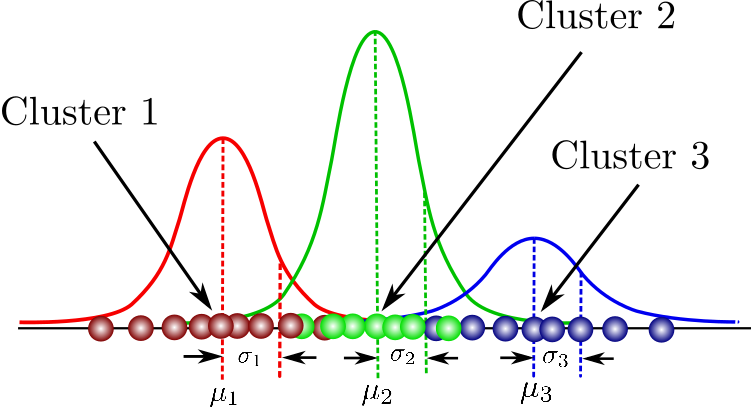
Las aplicaciones de aprendizaje automático también utilizan PDFs como parte de su enfoque para modelar la incertidumbre, optimizar los límites de clasificación y simular comportamientos probabilísticos, como los que se encuentran en Modelos de Mezcla Gaussiana (GMMs).

Aplicaciones de Modelado en Ingeniería y Ciencia

Los PDFs desempeñan un papel esencial en las tareas de ingeniería relacionadas con el análisis de fiabilidad. Por ejemplo, la ingeniería de fiabilidad a menudo sigue una distribución exponencial que el PDF ayuda a predecir probabilidades de fallas dentro de intervalos de tiempo particulares. Además, los PDFs juegan un papel vital en la conducción de sistemas basados en sensores donde el flujo de tráfico o las intensidades de señal siguen distribuciones de probabilidad específicas.

Los investigadores científicos utilizan frecuentemente PDFs en la investigación científica, especialmente para modelar el comportamiento de partículas en física. Las partículas cuánticas muestran densidades de probabilidad; usar PDFs permite a los científicos evaluar la probabilidad de que existan ciertas posiciones o momentos para cualquier particular partícula.

Diseño y Optimización en Sistemas del Mundo Real

Los PDFs se aplican eficazmente en la modelización de riesgos financieros para estimar la probabilidad de caídas extremas, pronósticos meteorológicos modelando variaciones de temperatura e incluso en juegos para asegurar distribuciones justas de recompensas o resultados. Por ejemplo, en el diseño de mecanismos de distribución de botines en videojuegos, funciones de distribución subyacentes balanceadas (representadas por PDFs) aseguran un juego justo y atractivo para los usuarios.

Malentendidos Sobre los PDFs y Aclaraciones

Malinterpretar los PDFs como Probabilidades Reales

Un malentendido común sobre los PDFs es confundir el valor \(f_X(x)\) con la probabilidad de que una variable aleatoria \(X\) sea igual a \(x\). Este malentendido surge porque las personas tienden a confundir la densidad en un solo punto con una probabilidad discreta. Sin embargo, para variables aleatorias continuas:

\(P(X = x) = 0\)

En lugar de proporcionar probabilidades para puntos específicos, los PDFs describen cómo esa probabilidad se distribuye a lo largo del rango de valores posibles.

Eventos de Probabilidad Cero No Significan Imposibilidad

Una aclaración importante es que mientras \(P(X = x) = 0\) para cualquier variable continua, esto no significa que la ocurrencia de \(X = x\) sea imposible. Simplemente refleja el hecho de que la posibilidad de aterrizar aleatoriamente en un valor exacto en una infi\(P(X = x) = 0\)nisura con precisión infinita. Sin embargo, la altura exacta, como 170.0000... cm, tiene probabilidad individual cero. En cambio, calculamos probabilidades sobre intervalos realistas, como \(P(169.9 \leq X \leq 170.1)\).

Al comprender este matiz, se puede interpretar y utilizar mejor los PDFs en una variedad de contextos sin caer en errores conceptuales comunes.

Aprovechando los PDFs para Entender las Distribuciones de Datos

Análisis de Densidades de Probabilidad en Datos

Las funciones de densidad de probabilidad (PDFs) proporcionan formas potentes de explorar las características de distribución de datos. Al observar su forma, uno puede obtener información clave sobre la dispersión, tendencia central y variabilidad de cualquier variable aleatoria.

Comparar el PDF de una distribución uniforme y una distribución normal revela variaciones significativas en la distribución de datos. Una distribución uniforme representa igual probabilidad en todos los valores, mientras que una distribución normal concentra las probabilidades cerca de su centro antes de disminuir hacia las colas.

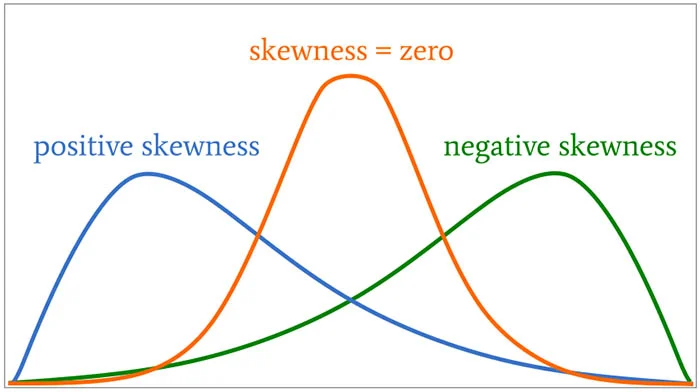
Los PDFs también permiten a los investigadores detectar sesgos y curtosis; tales distribuciones podrían indicar tendencias asimétricas dentro de los datos, mientras que la curtosis indica si las probabilidades se agrupan más cerca o más lejos de su promedio.

Visualización de PDFs como una Herramienta de Análisis de Datos

Imagina un gráfico de PDF similar a un mapa topográfico: su pico indica regiones donde los puntos de datos (o probabilidades) se acumulan con más frecuencia, mientras que los valles indican áreas más escasas. Superponiendo múltiples PDFs, los investigadores pueden comparar distribuciones de varios conjuntos de datos - por ejemplo, la distribución de ingresos entre grupos demográficos - revelando patrones, tendencias o anomalías que de otro modo permanecerían ocultos a la vista.

Visualizar PDFs junto con histogramas o estimaciones de densidad de núcleo (KDEs) permite a los practicantes pasar de descripciones matemáticas abstractas de conjuntos de datos a ideas más prácticas y accesibles sobre los datos.

Tipos Comunes de Distribuciones de Probabilidad y sus PDFs

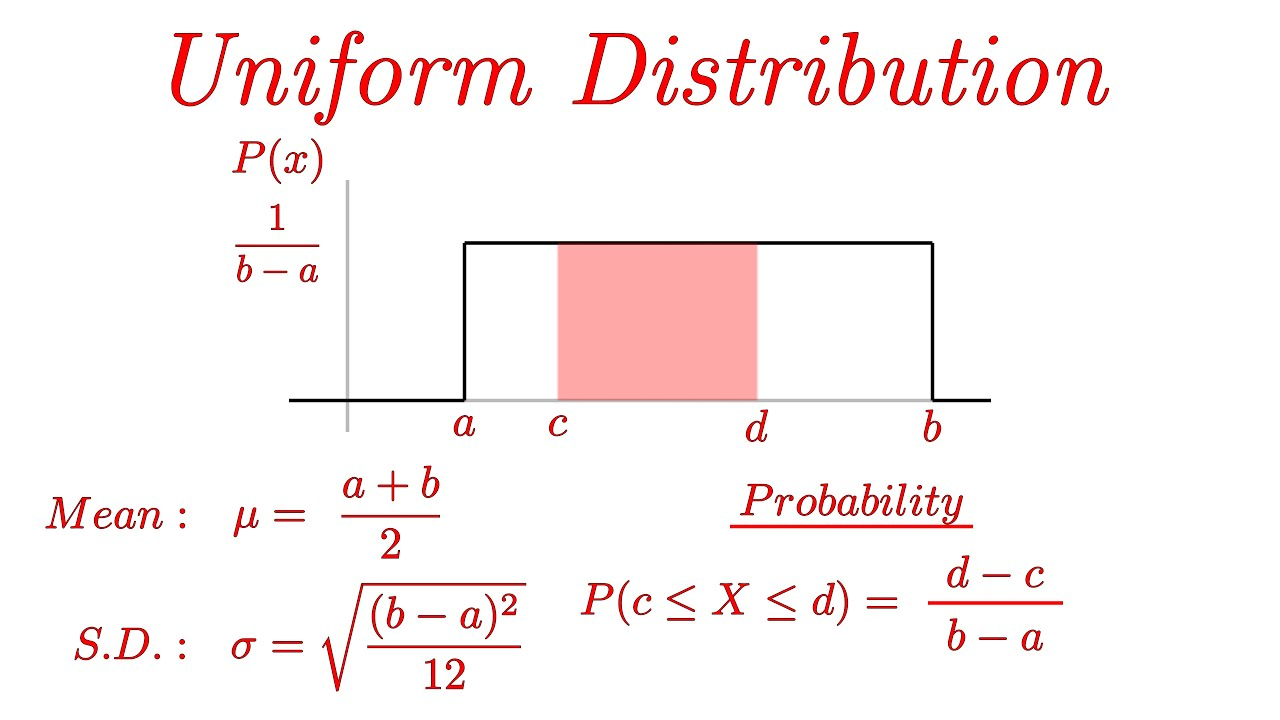
Distribución Uniforme

La distribución uniforme representa una variable aleatoria con probabilidades iguales a lo largo de un intervalo \([a, b]\). Su PDF se define como:

\(f_X(x) = \begin{cases} \frac{1}{b - a}, & \text{si } a \leq x \leq b \\ 0, & \text{en otro caso} \end{cases}\)

Por ejemplo, lanzar un dado justo puede modelarse como un análogo discreto a una distribución uniforme con iguales probabilidades a lo largo de los resultados.

Distribución Normal

La distribución normal (gaussiana), descrita por la curva en forma de campana, es una de las distribuciones más utilizadas. Su PDF es:

\(f_X(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x - \mu)^2 / (2\sigma^2)}\)

Aquí, \(\mu\) es la media y \(\sigma^2\) es la varianza. Esta distribución es fundamental en estadística debido al teorema del límite central, que establece que las medias muestrales de cualquier población tenderán a seguir una distribución normal.

Distribución Exponencial

La distribución exponencial es ampliamente utilizada en el modelado de confiabilidad y vida útil. Su PDF es:

\(f_X(x) = \begin{cases} \lambda e^{-\lambda x}, & \text{si } x \geq 0 \\ 0, & \text{en otro caso} \end{cases}\)

Aquí, \(\lambda\) determina la tasa de decaimiento, reflejando la probabilidad de que ocurra un evento en un marco de tiempo fijo, siendo útil en escenarios como fallos de maquinaria o sistemas de colas.

Conclusión

Las funciones de densidad de probabilidad (PDFs) forman una base esencial de la teoría de probabilidad continua, proporcionando el puente de ideas matemáticas abstractas a aplicaciones del mundo real. Al entender sus propiedades, su relación con las funciones de distribución acumulada (CDFs) y sus implicaciones prácticas, adquirimos herramientas para analizar conjuntos de datos, modelar incertidumbres y hacer predicciones.

Las PDFs ofrecen gran flexibilidad en aplicaciones de ingeniería, estadística y ciencia de datos, que van desde el procesamiento de señales hasta la evaluación del riesgo financiero. Al comprender sus principios fundamentales, como la normalización y la interpretación de la densidad, los usuarios pueden utilizar las PDFs de manera efectiva y manejar la aleatoriedad con confianza, haciendo de las PDFs herramientas indispensables para el estudio de fenómenos probabilísticos.

Referencia:

https://medium.com/towards-data-science/kernel-density-estimation-explained-step-by-step-7cc5b5bc4517 

https://libanswers.lib.miamioh.edu/stats-faq/faq/343628

https://en.wikipedia.org/wiki/Exponential_distribution