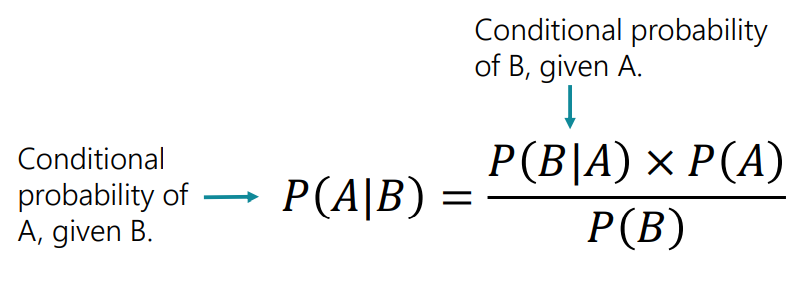¿Qué es la Probabilidad Condicional?
Aprende cómo la probabilidad condicional influye en las decisiones en industrias como la salud, las finanzas y la inteligencia artificial. Explora ejemplos del mundo real, el Teorema de Bayes y la optimización de decisiones.
Una Mirada Más Profunda a la Probabilidad Condicional
Definición e Importancia
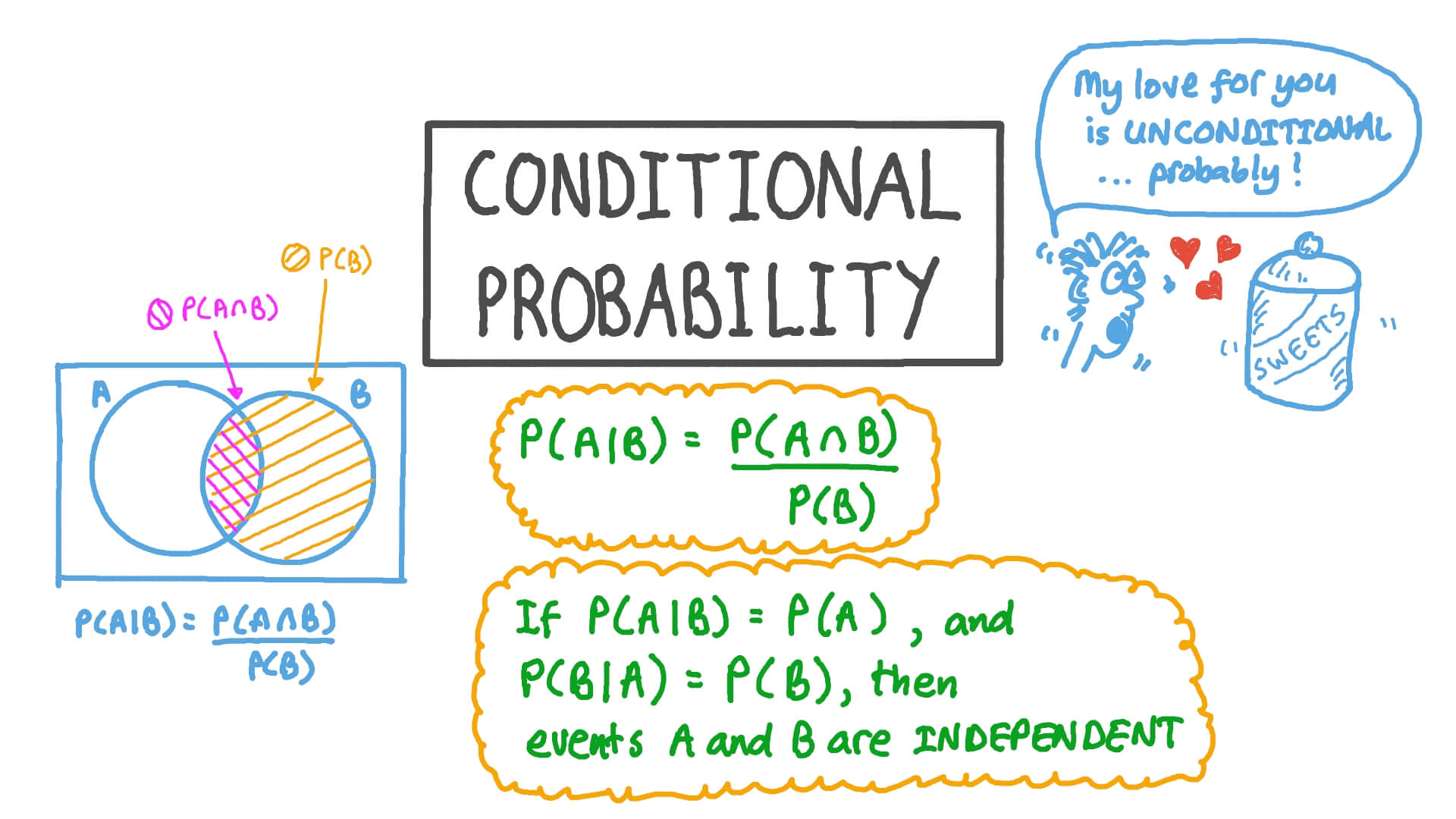
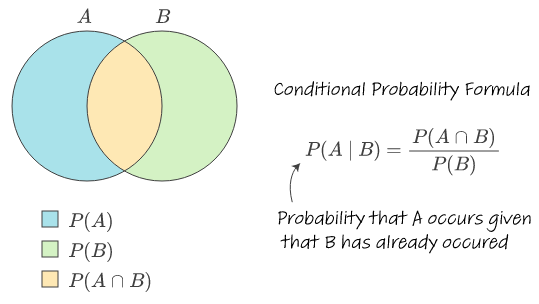
La probabilidad condicional se expresa matemáticamente como P(A|B), lo que se traduce como "la probabilidad de que ocurra A, dado que ha ocurrido B". La fórmula puede definirse como:
\(P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \quad \text{donde } P(B) \neq 0\)
Esto muestra cómo A (el evento dependiente) se determina dividiendo su probabilidad asociada por la de B (el evento condicionante).
La probabilidad condicional tiene aplicaciones de gran alcance en diversas industrias y problemas. Los médicos dependen de la probabilidad condicional al interpretar datos de pruebas, evaluando la probabilidad de que exista una enfermedad dadas los resultados de las pruebas diagnósticas; los analistas financieros utilizan probabilidades condicionales en modelos de análisis predictivo (por ejemplo, prediciendo movimientos de precios de acciones basándose en el rendimiento del sector); los algoritmos de inteligencia artificial/aprendizaje automático también usan probabilidades condicionales eficientemente al ajustar árboles de decisión, mejorando sistemas de clasificación y entrenando modelos predictivos de manera eficiente.
La probabilidad condicional es más que un concepto matemático abstracto: su poder reside en cuantificar las relaciones. Desde el seguimiento de patrones climáticos y políticas de salud pública, hasta la automatización de recomendaciones personalizadas de comercio electrónico y la automatización de recomendaciones personalizadas para productos en las tiendas en línea: la probabilidad condicional ofrece valiosas oportunidades de previsión y optimización.
Ejemplos Cotidianos
Una forma de entender las probabilidades condicionales es a través de escenarios familiares y sencillos:
1. Pronóstico del Tiempo: Imagina que te informan que solo hay un 30% de probabilidad de lluvia intensa en un día cualquiera; cuando las nubes cubren más del cielo de lo normal, los meteorólogos ajustan esta estimación al 70%. Así, la lluvia se vuelve contingente a la nubosidad, creando P(Lluvia|Nublado).
2. Diagnósticos Médicos: Suponiendo que, cuando son positivos, ciertas pruebas médicas indican un 80% de probabilidad de presencia de enfermedad; la probabilidad condicional puede entonces usarse para estimar esta probabilidad - P(Enfermedad|Prueba Positiva). Esto nos permite calcular la probabilidad de prevalencia de la enfermedad dado un resultado particular de la prueba.
3. Análisis del Mercado de Valores: Suponiendo que la acción A tiene un 60% de probabilidad de aumentar en valor, cuando los inversores observan altas tasas de crecimiento económico de, digamos, 5% o más, esta probabilidad salta al 85%, y la probabilidad condicional ayuda a los analistas de mercado a calcular relaciones como P(A|Alto Crecimiento).
Donde la Probabilidad Condicional Modela Decisiones
La fortaleza de la probabilidad condicional reside en su capacidad para transformar la dependencia entre eventos en ideas accionables. Los practicantes de aprendizaje automático usan probabilidades condicionales como base para árboles de decisión que reflejan procesos de toma de decisiones del mundo real influenciados por resultados anteriores; los urbanistas emplean análisis de delitos basados en probabilidades condicionales para estudiar patrones como el aumento de robos cuando disminuye la iluminación de las calles, por ejemplo.
Las empresas utilizan algoritmos predictivos para mejorar el comportamiento del cliente a través de recomendaciones personalizadas. Por ejemplo, una plataforma de comercio electrónico podría usar tu compra de zapatillas para correr (Evento B) como base para calcular si podrías comprar ropa deportiva (Evento A), respondiendo adecuadamente y personalizando las sugerencias en consecuencia.
La probabilidad condicional se ha convertido en una de las ideas revolucionarias de la matemática moderna debido a su amplia gama de usos fuera de los libros de texto.
Conceptos Clave en Probabilidad Condicional
Eventos Independientes vs. Dependientes
Al explorar la probabilidad condicional, un concepto fundamental gira en torno a diferenciar entre eventos independientes y dependientes. Esta distinción es crucial para entender cómo interactúan las probabilidades y por qué la probabilidad condicional se vuelve necesaria en ciertos escenarios.
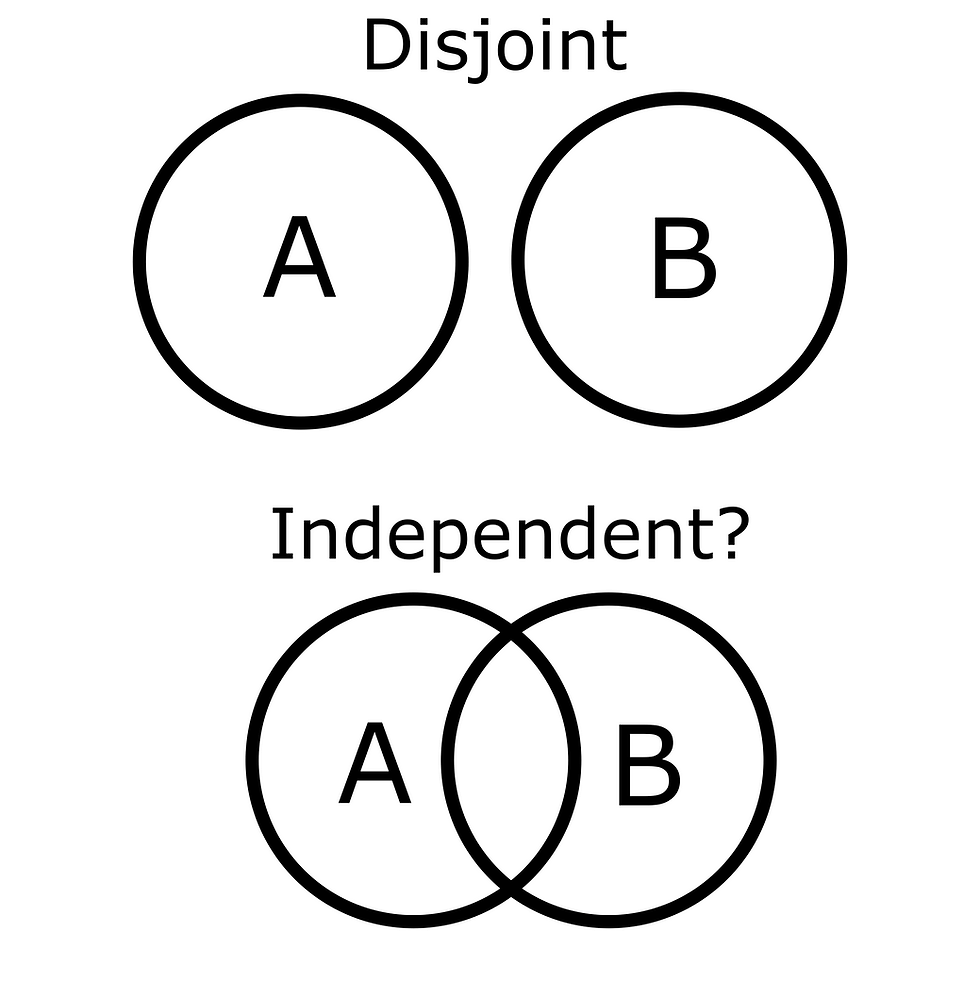
Eventos Independientes
Dos eventos se consideran independientes cuando el hecho de que uno ocurra no tiene efecto en la ocurrencia del otro. En tales casos, la probabilidad de que un evento ocurra no depende de ningún conocimiento previo del otro evento. La relación matemática para eventos independientes es:
\(P(A \cap B) = P(A) \cdot P(B)\)
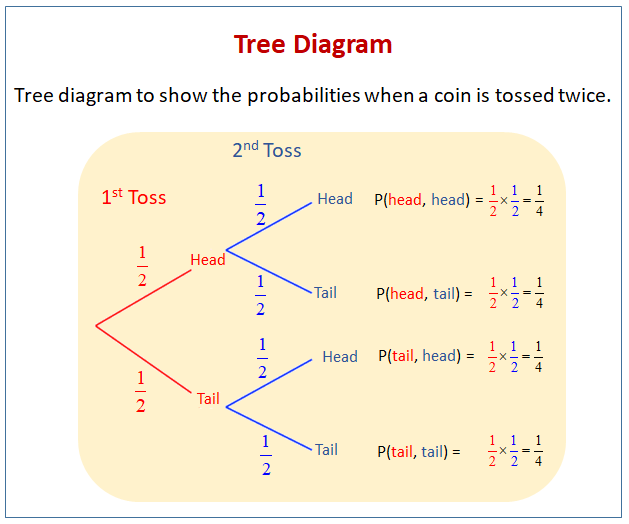
Como ejemplo, lanzar una moneda justa dos veces genera eventos independientes, donde el resultado del primer lanzamiento no influye en el resultado del segundo. Si la probabilidad de obtener cara es \(P(\text{Cara}) = 0.5\) para cada lanzamiento, entonces la probabilidad de obtener cara en ambos lanzamientos se calcula como:
\(P(\text{Cara, Cara}) = P(\text{Cara}) \cdot P(\text{Cara}) = 0.5 \cdot 0.5 = 0.25\)
Eventos Dependientes
Por otro lado, dos eventos son dependientes si la ocurrencia de uno altera la probabilidad del otro. La probabilidad condicional está diseñada específicamente para medir y manejar tales dependencias. Para eventos dependientes:
\(P(A \cap B) \neq P(A) \cdot P(B)\)
Por ejemplo, considere sacar dos cartas de un mazo estándar de 52 cartas sin reemplazo. La probabilidad de seleccionar un As (Evento A) durante el primer saque es:
\(P(A) = \frac{4}{52}\)
Una vez que se ha sacado un As, la composición del mazo cambia, alterando la probabilidad de sacar un Rey (Evento B) de las 51 cartas restantes. Esta dependencia hace que el Evento B sea condicional al Evento A.
Aplicaciones Reales de la Dependencia
La dependencia se puede observar en diversos campos. Por ejemplo:
En epidemiología, los modelos que predicen la transmisión de enfermedades infecciosas frecuentemente se basan en probabilidades dependientes derivadas de interacciones, tasas de vacunación o cambios en la densidad poblacional como indicadores de propagación.
Los actuarios de seguros utilizan probabilidades dependientes para calcular con precisión el riesgo; por ejemplo, en el caso de accidentes automovilísticos. Usan factores como el clima y las condiciones del tipo de carretera al hacer estimaciones de cuán probable es que ocurra un incidente.
Dependencia Híbrida en Modelos del Mundo Real
Los escenarios del mundo real a menudo exhiben una dependencia híbrida, un enfoque que llamamos multi-dependencia, en comparación con la dependencia total o la independencia. Tomemos, por ejemplo, la situación en la que un médico realiza dos pruebas de diagnóstico a un paciente para evaluar su condición usando diferentes pruebas diagnósticas cuyos resultados dependen parcialmente de los de la primera, así como de influencias externas como la historia del paciente o tendencias de datos poblacionales; hablando matemáticamente, estas situaciones necesitan modelos probabilísticos avanzados capaces de representar simultáneamente estas diferentes dependencias.
Fórmula y Notaciones de la Probabilidad Condicional
Para calcular correctamente las probabilidades condicionales, es esencial comprender su fórmula y las notaciones correspondientes.
Fórmula Estándar
La fórmula de la probabilidad condicional se origina de la conexión entre las probabilidades conjuntas y marginales:
\(P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \quad \text{donde } P(B) \neq 0\)
Aquí:
- \(P(A \mid B)\) representa la probabilidad condicional de que ocurra el Evento A dado que el Evento B ya ha ocurrido.
- \(P(A \cap B)\) denota la probabilidad conjunta de que ambos eventos A y B ocurran al mismo tiempo.
- \(P(B)\) es la probabilidad marginal del Evento B.
Esta fórmula nos muestra que para calcular la probabilidad condicional, necesitamos saber dos cosas:
1. La probabilidad de que ambos eventos ocurran juntos.
2. La probabilidad no condicionada del Evento B.
Para eventos dependientes, la fórmula actualiza la probabilidad base del Evento A en función de la nueva información relacionada con el Evento B.
Explicación de Notaciones de Probabilidad
Comprender los símbolos en la probabilidad condicional puede ser un reto, así que vamos a desglosarlos aquí:
1. \(P(A)\): La probabilidad simple o marginal de que ocurra el Evento A. Esto no considera ningún otro evento y se calcula de forma aislada. Ejemplo: La probabilidad de sacar un "4" en un dado justo de seis caras es:
\(P(4) = \frac{1}{6}\)
2. \(P(B \mid A)\): Representa el cálculo de probabilidad actualizado. Por ejemplo, la probabilidad de que salga cara, habiendo lanzado ya una moneda cargada a favor de cara:
\(P(\text{Cara} \mid \text{Moneda Cargada a Cara})\)
3. \(P(A \cap B)\): La probabilidad conjunta se refiere a la ocurrencia simultánea de ambos eventos A y B. Por ejemplo, en un mazo de cartas, la probabilidad de sacar un Rey y un As en dos extracciones consecutivas sin reemplazo:
\(P(\text{Rey} \cap \text{As}) = P(\text{Rey}) \cdot P(\text{As} \mid \text{Rey})\)
Flexibilidad del Uso de la Fórmula
La probabilidad condicional es increíblemente versátil y tiene aplicaciones flexibles en todos los sectores. Por ejemplo, los analistas financieros pueden calcular \(P(\text{Incremento de Ganancias} \mid \text{Crecimiento Positivo de la Industria})\) para evaluar el rendimiento de acciones.
Probabilidad Condicional como un "Marco Bayesiano"
La probabilidad condicional proporciona la base para poderosos marcos como el Teorema de Bayes y la inferencia bayesiana, utilizando la probabilidad condicional para actualizar constantemente las predicciones en función de nuevas evidencias. Por ejemplo, las aplicaciones de navegación en tiempo real ajustan las recomendaciones de rutas \(P(\text{Mejor Ruta} \mid \text{Congestión Actual})\) cada vez que llegan nuevos datos de tráfico.
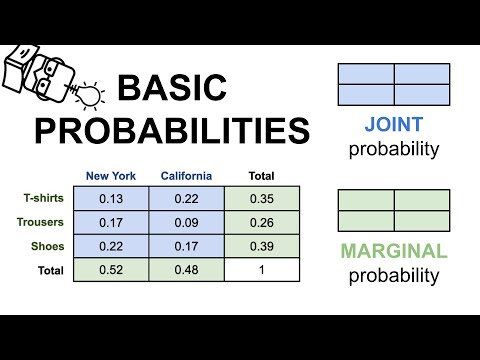
Probabilidad Condicional vs. Otros Tipos de Probabilidades
Las probabilidades son herramientas versátiles que vienen en muchas formas dependiendo de lo que se esté midiendo. La probabilidad condicional se destaca porque introduce el concepto de dependencia, pero para comprender completamente su significado; debemos explorar cómo contrasta con otros tipos de probabilidades, a saber, marginales y conjuntas.
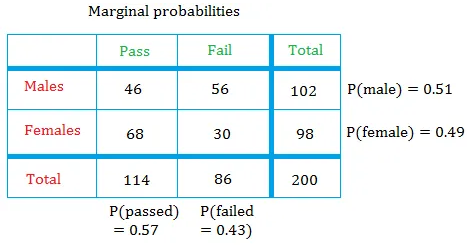
Probabilidad Marginal
La probabilidad marginal representa la probabilidad de que ocurra un solo evento por sí solo sin considerar otros eventos. Es el tipo más simple de probabilidad y a menudo se representa como \(P(A)\) o \(P(B)\). Por ejemplo:
- La probabilidad de sacar un As de una baraja estándar de cartas es:
\(P(\text{As}) = \frac{4}{52} = \frac{1}{13}\)
Las probabilidades marginales proporcionan la base de la teoría de la probabilidad. Se llaman probabilidades marginales porque sus sumatorias son sobre todos los resultados posibles de otra variable aleatoria.
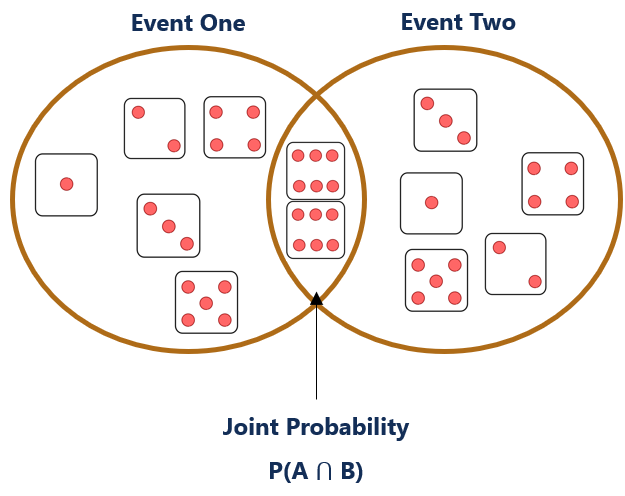
Probabilidad Conjunta
La probabilidad conjunta, por otro lado, describe la probabilidad de que dos o más eventos ocurran al mismo tiempo. Se representa matemáticamente como \(P(A \cap B)\), donde \(A\) y \(B\) son los eventos de interés. Por ejemplo:
- La probabilidad de sacar un As rojo de una baraja estándar de cartas es:
\(P(\text{Rojo} \cap \text{As}) = \frac{2}{52} = \frac{1}{26}\)
A diferencia de la probabilidad marginal, la probabilidad conjunta examina la superposición de dos eventos. Asume que ambos eventos ocurren juntos, y esta superposición es particularmente importante cuando se trabaja con resultados correlacionados.
Análisis Comparativo: Probabilidad Marginal, Conjunta y Condicional
La principal distinción entre estos tipos de probabilidad radica en cómo se tratan las dependencias:
1. Probabilidad Marginal: Independiente de otras condiciones o eventos, esta medida representa la probabilidad absoluta.
2. Probabilidad Conjunta: Evalúa la probabilidad de que dos o más eventos ocurran simultáneamente y, por lo tanto, considera su interacción.
3. Probabilidad Condicional: La probabilidad condicional es una extensión de ambos métodos, explicando cómo un evento afecta a otro en relación con ellos. A diferencia de la probabilidad conjunta, su principal preocupación radica en cómo un evento cambia su probabilidad más que en la co-ocurrencia como tal.
El Modelo de "Pastel en Capas" de Probabilidad
Una analogía efectiva para entender estas relaciones es el modelo de "pastel en capas":
Capa Base: Probabilidades marginales que proporcionan una comprensión de resultados individuales como conceptos fundamentales.
Capa Media: Probabilidades conjuntas, representadas como rebanadas que se entrelazan entre capas para representar eventos que ocurren simultáneamente;
Capa Superior: Probabilidades condicionales que cortan y dividen el pastel más precisamente dependiendo de la información disponible.
Supón que estás realizando un análisis para una tienda en línea. Tu capa base podría consistir en probabilidades marginales para comprar cualquier artículo; tu capa media podría examinar compras simultáneas (por ejemplo, comprar zapatos y calcetines a la vez); finalmente, tu capa superior podría centrarse en dependencias específicas (es decir, la probabilidad de comprar calcetines dado que ya se compraron zapatos).
Adoptar un enfoque iterativo ayuda a contextualizar la probabilidad condicional como una herramienta analítica que enfoca mientras toma en cuenta el conocimiento externo para tomar decisiones informadas.
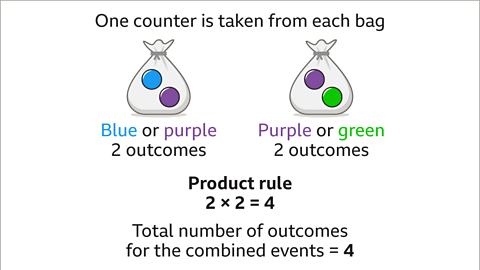
Diagramas de Árboles y la Regla de Multiplicación
Los diagramas de árboles y la regla de multiplicación juegan roles esenciales en la visualización y simplificación de cálculos de probabilidad de múltiples pasos. Juntos, proporcionan claridad para resolver escenarios más complejos de probabilidad condicional.
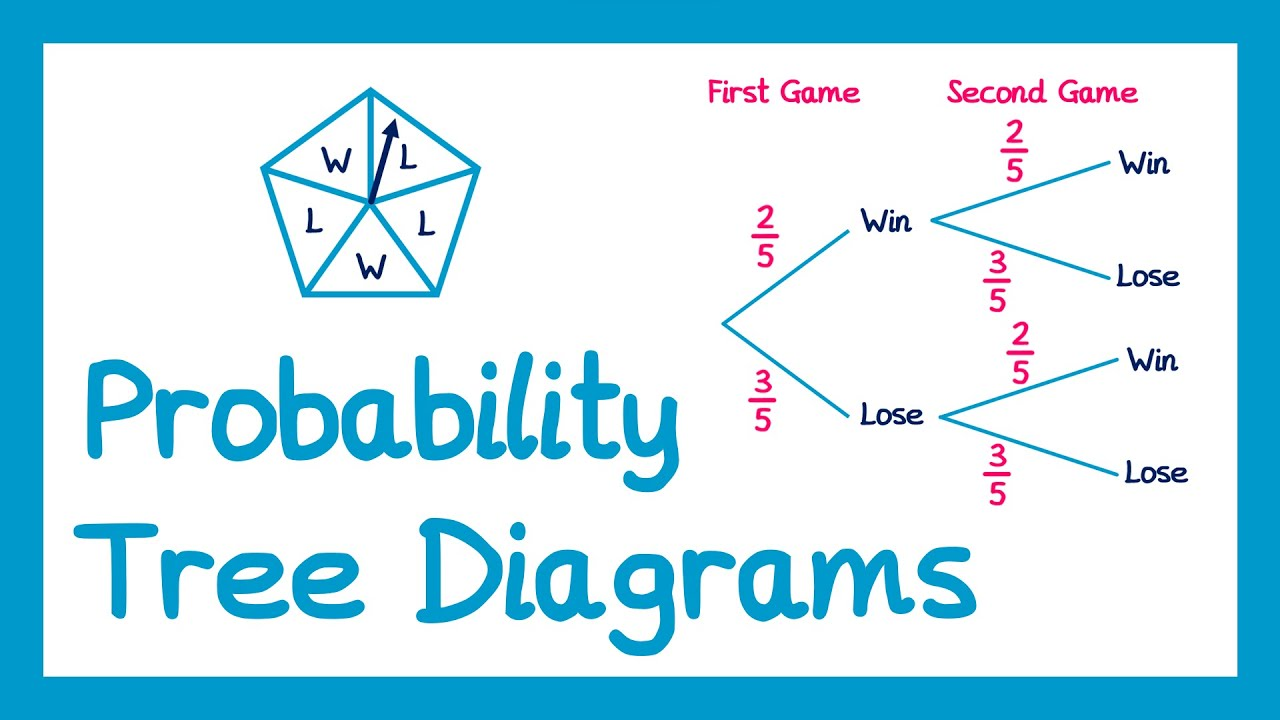
Cómo Funcionan los Diagramas de Árboles
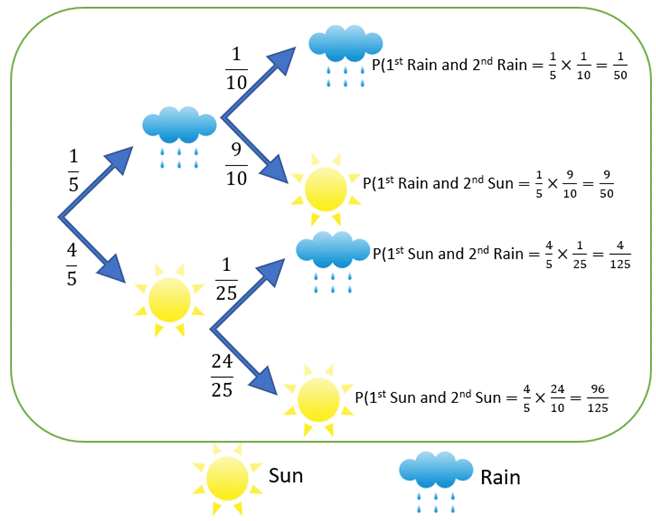
Un diagrama de árbol es una representación visual ramificada utilizada para mapear sistemáticamente las probabilidades de eventos secuenciales. Cada rama representa un posible resultado, y siguiendo las probabilidades de las vías paso a paso, se pueden calcular tanto probabilidades simples como condicionales.
Ejemplo: Diagrama de Árbol Básico
Suponga que está analizando un escenario de dos pasos: lanzar una moneda justa y luego lanzar un dado de seis caras. Los resultados se pueden mapear de la siguiente manera:
1. Paso 1: Los resultados de la moneda (Cara o Cruz) tienen una probabilidad de \(0.5\).
2. Paso 2: Para cada rama (Cara o Cruz), los resultados del dado varían de 1 a 6 con probabilidades \(\frac{1}{6}\).
El árbol tendría 12 ramas en total, cada una terminando en un evento único, como "Cara-3" o "Cruz-5." Las probabilidades de resultados específicos se pueden calcular multiplicando las probabilidades a lo largo de cada rama.
Beneficio de la Visualización
Los diagramas de árboles simplifican el razonamiento probabilístico dividiéndolo en pasos manejables. Permiten visualizar las dependencias de los eventos y reducir errores manuales.
Incorporando la Regla de Multiplicación en Diagramas de Árboles
La Regla de Multiplicación vincula las probabilidades conjuntas a las probabilidades condicionales:
\(P(A \cap B) = P(A) \cdot P(B \mid A)\)
Esta fórmula es especialmente útil para calcular probabilidades en escenarios secuencialmente dependientes. Por ejemplo:
- Suponga que un frasco contiene cinco caramelos rojos y tres azules. Si se saca un caramelo sin reemplazo, el diagrama de árbol de probabilidad presentará lo siguiente:
- Primer Sorteo: Rojo (\(P(R_1) = \frac{5}{8}\)) y Azul (\(P(B_1) = \frac{3}{8}\)).
- Segundo Sorteo: Las probabilidades dependientes para resultados subsecuentes (por ejemplo, \(P(R_2 \mid R_1)\)) se ajustan según lo que se sacó primero. Estas probabilidades condicionales capturan la dependencia entre los sorteos.
Aplicaciones Reales de los Diagramas de Árboles y la Regla de Multiplicación
En la práctica, los diagramas de árboles a menudo modelan:
- Diagnósticos Médicos: Calcular errores o éxitos de pruebas de múltiples etapas.
- Carteras de Inversión: Evaluar ganancias o pérdidas paso a paso a través de escenarios financieros interdependientes.
- Juegos de Mesa: Diseñar probabilidades del jugador en juegos de múltiples turnos (por ejemplo, Monopolio).
Diagramas de Árboles como Herramientas de Depuración de Probabilidades
Los diagramas de árboles van más allá de simplemente calcular probabilidades - también nos permiten detectar errores en el razonamiento. Por ejemplo:
Los diagramas de árboles pueden ayudar a resolver problemas de probabilidad al ayudar a modelar correctamente todos los posibles caminos para garantizar claridad y precisión en los cálculos. Permiten claridad sobre la complejidad.
Los diagramas de árboles pueden ser particularmente efectivos para diagnosticar fallas del sistema al descubrir "ramas olvidadas," como un mal funcionamiento del hardware, que de otro modo pasarían desapercibidas y distorsionarían los cálculos de fiabilidad total.
Así, los diagramas de árboles no solo sirven como ayudas computacionales sino que también son poderosas herramientas conceptuales para comprender probabilidades a través de múltiples pasos.
Probabilidad Condicional y el Teorema de Bayes
La probabilidad condicional sirve como la base para el Teorema de Bayes, un principio que nos permite invertir o actualizar probabilidades a la luz de nueva evidencia.
Introducción al Teorema de Bayes
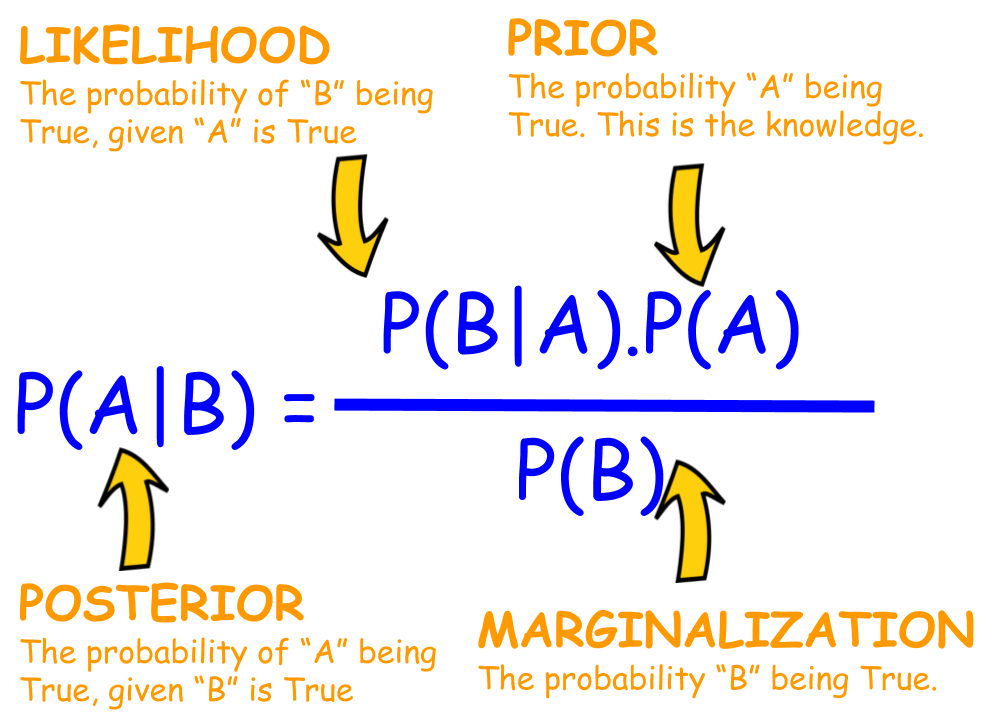
El Teorema de Bayes reconfigura matemáticamente la probabilidad condicional:
\(P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}, \quad \text{donde } P(B) \neq 0\)
Donde:
- \(P(A \mid B)\): La probabilidad actualizada de \(A\) ocurriendo dado \(B\).
- \(P(A)\): La probabilidad previa o de base de \(A\).
- \(P(B \mid A)\): La probabilidad de \(B\) dado que \(A\) ha ocurrido.
- \(P(B)\): La probabilidad marginal de \(B\) ocurriendo en general.
El teorema es particularmente poderoso cuando los cálculos directos de \(P(A \mid B)\) son difíciles, pero probabilidades relacionadas como \(P(B \mid A)\) son más fáciles de evaluar.
Aplicaciones Prácticas
El Teorema de Bayes sobresale en una variedad de contextos del mundo real:
Diagnósticos en Salud
Utilizando \(P(\text{Enfermedad} \mid \text{Prueba Positiva})\) para evaluar la probabilidad de tener una enfermedad dado un resultado positivo. Ajustando según la precisión de la prueba (\(P(\text{Prueba Positiva} \mid \text{Enfermedad})\)) y prevalencia de la enfermedad (\(P(\text{Enfermedad})\)), los médicos pueden hacer mejores diagnósticos.
Filtrado de Spam
Los algoritmos de correo electrónico predicen la probabilidad de que un correo sea spam (\(P(\text{Spam} \mid \text{Palabras Sospechosas})\)) al analizar las frecuencias de palabras.
Conducción Autónoma
Los sistemas estiman los riesgos de conducción usando enfoques bayesianos donde nueva evidencia (\(B\)), como condiciones del camino, actualizan continuamente las probabilidades de accidentes (\(P(\text{Accidente} \mid B)\)).
Más allá de Actualizaciones Estáticas
El Teorema de Bayes también es crucial en sistemas dinámicos. Por ejemplo, los pronósticos del tiempo son continuamente refinados usando actualizaciones de satélites en tiempo real. Las probabilidades basadas en modelos iniciales \(P(\text{Lluvia} \mid \text{Cielo})\) se revisan cada hora basándose en nuevos datos satelitales.
Pensamiento Bayesiano en Inteligencia Artificial
La importancia del Teorema de Bayes se extiende más allá de las matemáticas hacia la psicología y la inteligencia artificial (IA). Los humanos a menudo tienen dificultades para razonar con precisión sobre probabilidades debido a sesgos cognitivos, pero los sistemas de IA impulsados por modelos bayesianos sobresalen al superar estas limitaciones.
Por ejemplo:
- Motores de Recomendación: Netflix sugiere películas usando probabilidades \(P(\text{Gustar} \mid \text{Preferencias de Género})\) influenciadas por el historial de visualización.
- Clasificadores de Spam: Los filtros bayesianos enfrentan patrones sofisticados de spam al aprender continuamente \(P(\text{Spam} \mid \text{Patrones de Estafas Engañosas})\) y adaptarse.
El Teorema de Bayes conecta la evidencia pasada con el conocimiento actualizado, ayudando a los algoritmos a tomar decisiones en entornos cambiantes más rápidamente y de forma más precisa que la intuición humana.
Aplicaciones de la Probabilidad Condicional en la Vida Real
La probabilidad condicional es más que un concepto académico; sus aplicaciones en el mundo real se extienden a través de diversas industrias. Desde la predicción de enfermedades hasta la optimización de estrategias financieras, comprender las dependencias entre eventos ha proporcionado conocimientos útiles que informan áreas clave de la toma de decisiones.
Salud y Diagnóstico
En el campo médico, la probabilidad condicional es una piedra angular del análisis diagnóstico. Los profesionales de la salud analizan rutinariamente los resultados de pruebas de pacientes para inferir la probabilidad de una enfermedad dada la presencia de síntomas específicos o resultados de pruebas.
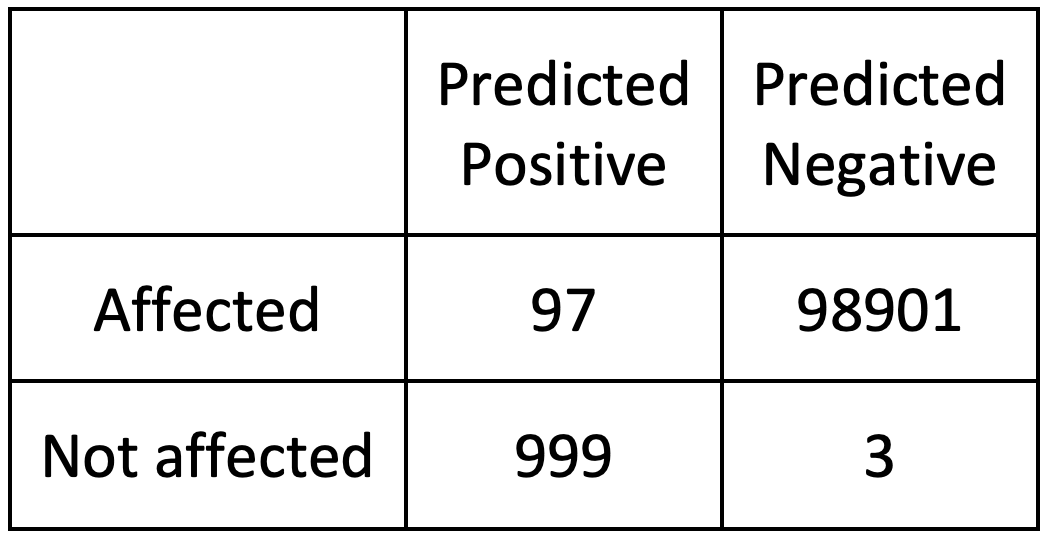
Ejemplo: Diagnóstico de Enfermedades
Supongamos que una prueba de sangre para una enfermedad tiene un 95% de sensibilidad (tasa de verdaderos positivos) y un 85% de especificidad (tasa de verdaderos negativos). Si la prevalencia general de la enfermedad en la población es del 1%, el Teorema de Bayes puede utilizarse para calcular la probabilidad de realmente tener la enfermedad dado un resultado positivo (\(P(\text{Disease} \mid \text{Positive Test})\)). Esto considera la precisión de la prueba y la prevalencia de la enfermedad, guiando a los médicos a evitar una falsa sensación de certeza en condiciones de baja prevalencia.
Tales cálculos son primordiales durante pandemias, donde interpretar los resultados de las pruebas ayuda a dirigir medidas de contención de manera efectiva.
Gestión de Riesgos Financieros
La industria financiera aprovecha la probabilidad condicional para cuantificar y mitigar riesgos de mercado, calcular calificaciones crediticias y optimizar inversiones. Por ejemplo:
- Incumplimiento de Préstamos: Los bancos pueden evaluar la probabilidad de que un prestatario incumpla un préstamo (\(P(\text{Default} \mid \text{Bad Credit History})\)). Al considerar probabilidades condicionadas por historial crediticio, niveles de ingresos y situación laboral, las instituciones financieras crean políticas de préstamo más confiables.
- Análisis de Riesgo de Carteras: Las firmas de inversión calculan las probabilidades del rendimiento de acciones bajo ciertas condiciones económicas, como \(P(\text{Stock Rise} \mid \text{GDP Growth})\). Esto ayuda a estructurar carteras que se protegen contra dependencias.
Pronóstico Ambiental
La probabilidad condicional se utiliza ampliamente en las ciencias ambientales para predecir el clima y desastres naturales. Por ejemplo:
- Predicción de Inundaciones: Ingenieros y científicos ambientales analizan la probabilidad de inundaciones (\(P(\text{Flood} \mid \text{Heavy Rainfall})\)) basándose en condiciones de lluvia y factores geográficos.
- Modelado Climático: Estimaciones como \(P(\text{Temperature Increase} \mid \text{Carbon Dioxide Levels})\) informan políticas globales sobre cómo abordar el cambio climático.
Probabilidad Condicional en Automatización de Decisiones
Una de las aplicaciones más vanguardistas de la probabilidad condicional se encuentra en los sistemas de toma de decisiones autónomas. Los algoritmos en autos autónomos estiman riesgos de manera dinámica. Por ejemplo:
- \(P(\text{Collision} \mid \text{Traffic Flow})\) permite a los sistemas a bordo predecir y actuar ante peligros inminentes basándose en datos en tiempo real.
- Los sistemas inteligentes también optimizan rutas de entrega usando predicciones condicionales, como \(P(\text{Delay} \mid \text{Rain in City X})\).
A través de las industrias, la síntesis de probabilidades condicionadas a datos contextuales alimenta algoritmos de toma de decisiones, automatizando tareas que antes eran gobernadas por la discreción humana.
Problemas Complejos y Conceptos Erróneos Comunes
La probabilidad condicional puede ser sorprendentemente intuitiva cuando se aplica a escenarios simples, pero las situaciones de la vida real a menudo presentan desafíos. Además, los conceptos erróneos sobre la probabilidad condicional pueden llevar a errores en el análisis y la toma de decisiones.
Problemas Desafiantes
Los problemas del mundo real en probabilidad condicional a menudo involucran situaciones complejas con múltiples condiciones que interactúan, lo que requiere una preparación cuidadosa y un cálculo para asegurar que no se pase por alto ningún aspecto crucial.
Ejemplo: Dependencias de Múltiples Niveles
Considere lanzar tres dados simultáneamente y calcular la probabilidad de obtener al menos un "6," dado que la suma de los dados es impar. Este problema introduce interdependencias que no son inmediatamente obvias. Cada lanzamiento de dado afecta la suma del conjunto (\(P(\text{Suma Impar})\)), y esto, a su vez, cambia la probabilidad para resultados individuales como obtener un "6." Se requiere un desglose paso a paso para evitar errores, dividiendo el problema en partes condicionales manejables.
Ejemplo: Eventos Combinados
Calcular las probabilidades de combinaciones complejas como sacar dos As seguidos de un Rey sin reemplazo puede ser complicado en juegos de cartas, lo que hace que el cálculo directo sea desafiante.
Los diagramas de árbol y la aplicación sistemática de las fórmulas \(P(A \mid B)\) y \(P(B \mid A)\) se vuelven esenciales en estos casos.
Conceptos Erróneos y Errores
Los conceptos erróneos con respecto a la probabilidad condicional surgen con frecuencia como resultado de confundirla con otros tipos de probabilidad o malinterpretar su relación con la dependencia de eventos.
Intercambio de Probabilidades Conjuntas y Condicionales
Muchos errores surgen al interpretar \(P(A \cap B)\) (probabilidad conjunta) como \(P(A \mid B)\) o viceversa, resultando en conclusiones erróneas. Este concepto erróneo aparece a menudo en áreas como las pruebas médicas, donde no diferenciar entre \(P(\text{Enfermedad} \cap \text{Prueba Positiva})\) y \(P(\text{Enfermedad} \mid \text{Prueba Positiva})\) podría conducir a diagnósticos engañosos.
Asumir Independencia Sin Verificación
Un error común es asumir que dos eventos son independientes cuando, de hecho, son dependientes. Por ejemplo, al analizar tendencias del mercado, asumir \(P(\text{Subida Acciones A} \cap \text{Caída Acciones B}) = P(\text{Subida Acciones A}) \cdot P(\text{Caída Acciones B})\) ignora las posibles dependencias entre las dos acciones, llevando a pronósticos incorrectos.
Escenarios de Usos Incorrectos de Probabilidades Condicionales
Un escenario frecuentemente mal utilizado involucra la confusión entre correlación y causalidad. Por ejemplo:
- Los estudios podrían sugerir que \(P(\text{Enfermedad Cardíaca} \mid \text{Consumo de Alcohol})\) es alta en ciertos grupos demográficos. Sin embargo, interpretar esto como causalidad podría ignorar dependencias compartidas, como \(P(\text{Enfermedad Cardíaca} \mid \text{Patrones Dietéticos})\), confundiendo análisis y recomendaciones políticas.
A través de los dominios, entender el significado preciso e implicaciones de las probabilidades condicionales es crítico para evitar errores y sesgos que hagan un mal uso de los datos.
Conclusión
La probabilidad condicional es un concepto práctico e impactante que nos permite interpretar la probabilidad de eventos en el contexto de dependencias. Herramientas como el teorema de Bayes, los diagramas de árbol y la regla de multiplicación equipan a individuos y sistemas automatizados para realizar predicciones confiables y tomar decisiones informadas.
La probabilidad condicional tiene numerosas aplicaciones en ámbitos como salud, finanzas e IA que demuestran su utilidad para resolver problemas del mundo real y optimizar resultados. Su uso adecuado requiere distinguir entre independencia, correlación y causalidad para evitar interpretaciones erróneas de las estimaciones de probabilidad condicional.
El dominio de la probabilidad condicional es crítico en un mundo cada vez más interdependiente y basado en datos, ayudando a las personas a abordar incertidumbres de manera efectiva mientras toman decisiones racionales y fundamentadas en datos de manera eficiente.
Referencia:
https://www.amazon.com/Signal-Noise-Many-Predictions-Fail-but/dp/0143125087