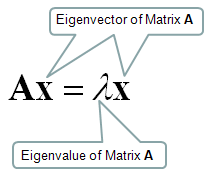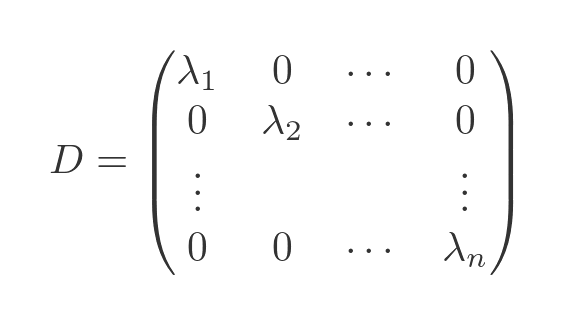Cómo diagonalizar una matriz: Una guía completa
Aprende diagonalización de matrices con autovalores y autovectores. Simplifica cálculos complejos, resuelve ecuaciones diferenciales y evita errores en aplicaciones de física/ciencia de datos.
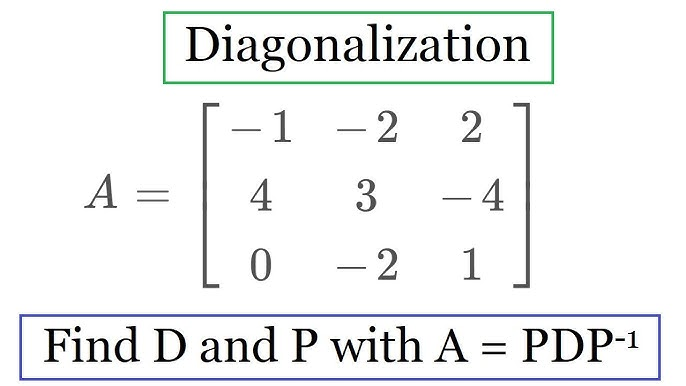
¿Qué es la Diagonalización de Matrices?
La diagonalización es el proceso de simplificar una matriz cuadrada transformándola en una matriz diagonal, donde todos los elementos fuera de la diagonal se convierten en cero. Una matriz \(A\) es diagonalizable si existe una matriz invertible \(S\) y una matriz diagonal \(D\) tal que \(S^{-1}AS = D\). Los elementos diagonales de \(D\) son los valores propios de \(A\), y las columnas de \(S\) son los vectores propios de \(A\). Esta técnica es sumamente útil en el álgebra lineal porque las matrices diagonales son más sencillas de manejar, ya que operaciones como potencias de matrices y exponenciales se vuelven directas.
La diagonalización de matrices juega un papel esencial en muchas aplicaciones, desde resolver sistemas de ecuaciones diferenciales lineales y análisis de sistemas mecánicos, hasta disminuir la complejidad computacional para algoritmos de ciencia de datos. Al entender las técnicas de diagonalización, tanto estudiantes como profesionales pueden descubrir maneras elegantes y eficientes de manipular matrices para abordar problemas del mundo real de manera más eficiente.
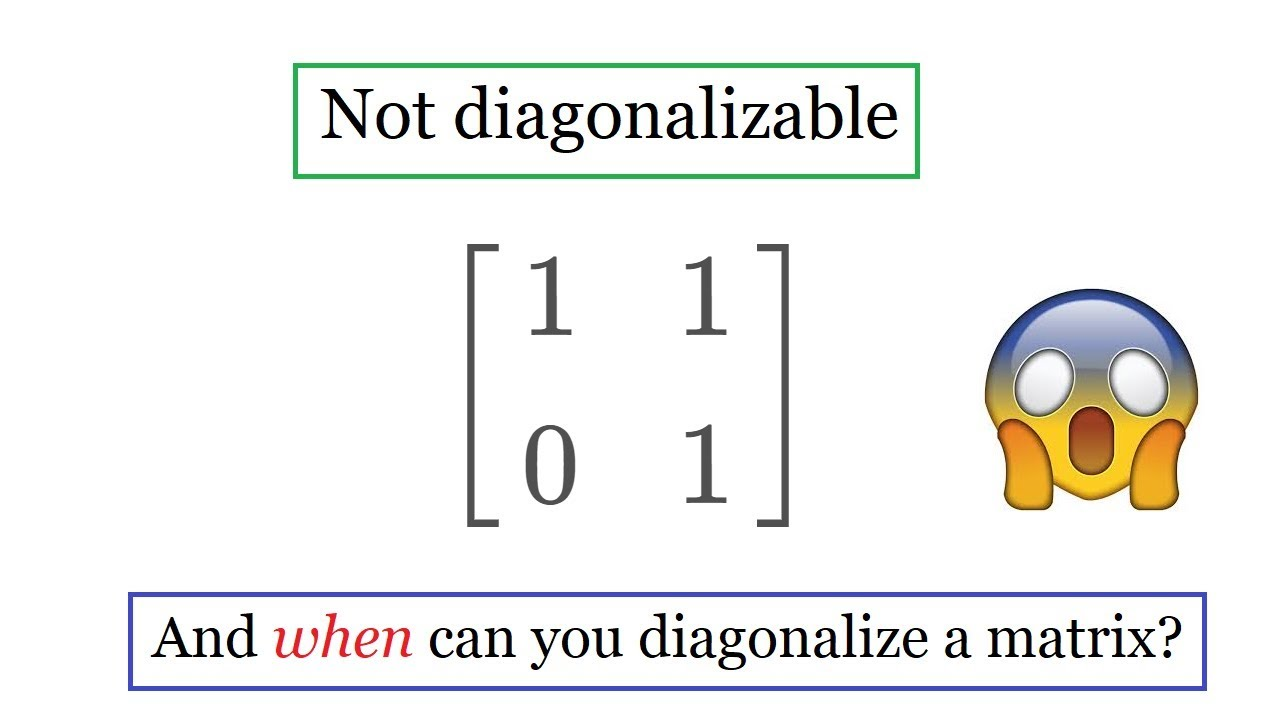
¿Cuándo se Puede Diagonalizar una Matriz?
No todas las matrices pueden ser diagonalizadas. Para ser diagonalizable, una matriz debe tener suficientes vectores propios linealmente independientes que abarquen su espacio de manera efectiva - específicamente igualando su multiplicidad geométrica (es decir, dimensión de su espacio propio) con su multiplicidad algebraica (número de veces que su valor aparece como raíces en polinomios característicos); de lo contrario, las matrices defectuosas no pueden ser diagonalizadas.
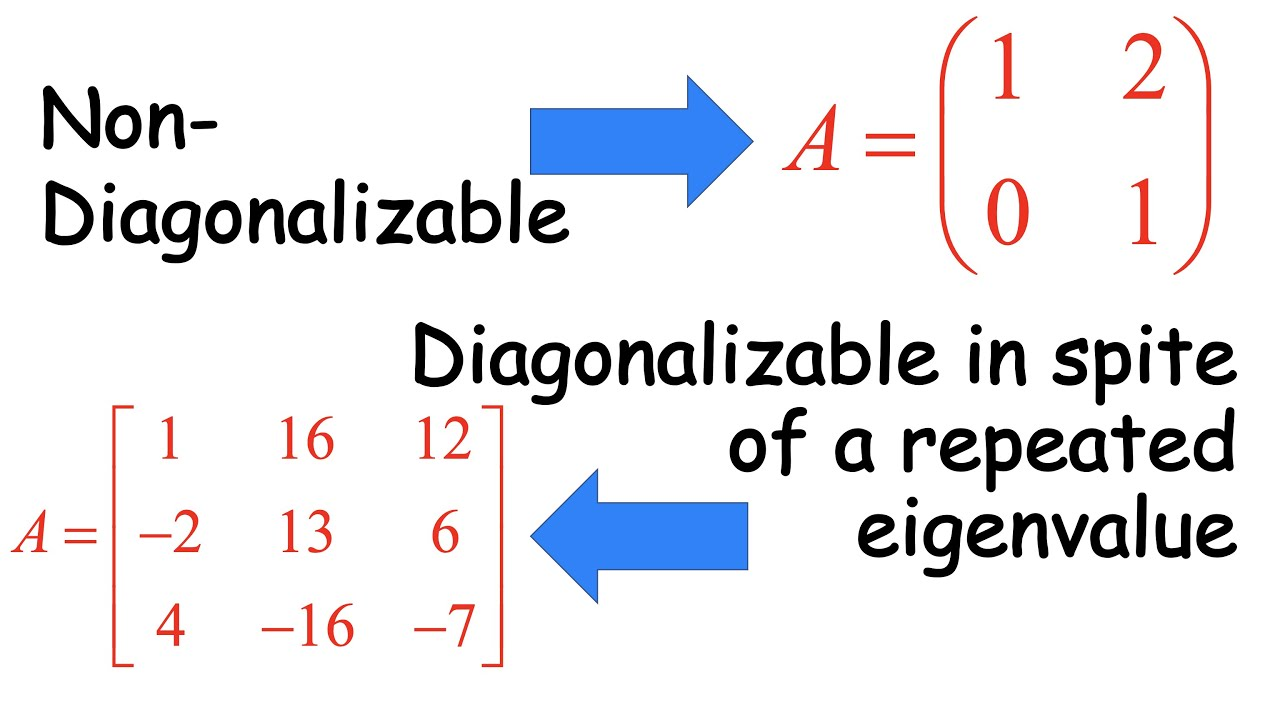
Las matrices con valores propios distintos siempre pueden ser diagonalizadas; sin embargo, aquellas que contienen valores propios repetidos pueden o no cumplir esta condición dependiendo de los espacios propios que ocupan; las matrices cuadradas defectuosas no pueden cumplir tales condiciones para la diagonalización.
Conceptos Clave Detrás de la Diagonalización
Valores y Vectores Propios
Los conceptos de valores y vectores propios son fundamentales en la diagonalización de matrices.
- Valores propios: Si una matriz \(A\) actúa sobre un vector \(v\), y el resultado es un múltiplo escalar de \(v\), entonces \(v\) se denomina vector propio, y el escalar \(\lambda\) se denomina valor propio. Formalmente:
\(Av = \lambda v\)
Reordenando se obtiene \((A - \lambda I)v = 0\), donde \(I\) es la matriz identidad. Encontrar los valores propios requiere resolver la ecuación característica, \(\text{det}(A - \lambda I) = 0\), que proporciona los valores propios como las raíces de la ecuación del determinante.
- Vectores propios: Para cada valor propio \(\lambda\), sus vectores propios se encuentran en el espacio nulo (núcleo) de \(A - \lambda I\). Estos vectores propios definen "direcciones" a lo largo de las cuales la transformación lineal \(A\) estira o comprime vectores por un factor de \(\lambda\).
Analogía ilustrativa: Imagina estirar un resorte en varias direcciones hasta que ciertas direcciones experimentan estiramiento o compresión sin alterar su orientación; estos son conocidos como vectores propios, y sus cantidades constituyen sus valores propios; los ingenieros mecánicos a menudo utilizan este concepto al estudiar análisis de estrés o vibración, mientras que en el aprendizaje automático, el Análisis de Componentes Principales (PCA) se basa en ellos para la determinación de varianza de datos.
Polinomio Característico y su Rol
Para diagonalizar una matriz \(A\), primero debes calcular sus valores propios resolviendo el polinomio característico:
\(p(t) = \text{det}(A - tI)\)
Aquí, \(A - tI\) se refiere a la matriz \(A\), donde \(t\) actúa como un marcador de posición para los valores propios a lo largo de la diagonal de la matriz identidad \(I\). El determinante proporciona una ecuación polinómica, y resolver \(p(t) = 0\) produce los valores propios de \(A\).
- Multiplicidad algebraica: Este es el número de veces que una raíz (valor propio) aparece en \(p(t)\).
- Multiplicidad geométrica: Representa la dimensión del espacio propio o el número de vectores propios linealmente independientes asociados con un valor propio particular.
Para la diagonalización, la condición esencial es que la multiplicidad geométrica = multiplicidad algebraica para todos los valores propios. Si esta condición no se satisface, la matriz es defectuosa y no puede ser diagonalizada.
Transformaciones de Similitud
Matriz diagonalización se basa en el concepto de transformaciones de similitud. Dos matrices \(A\) y \(B\) se consideran similares si existe una matriz invertible \(S\) tal que:
\(B = S^{-1}AS\)
En el caso de la diagonalización, \(B\) se convierte en la matriz diagonal \(D\), y \(S\) contiene los vectores propios de \(A\) como sus columnas.
Propiedades Mantenidas Bajo Transformaciones de Similitud:
- Determinante
- Trazar (suma de los elementos diagonales)
- Rango
- Valores propios (pero no vectores propios)
La investigación de la similitud es crítica porque la descomposición de valores propios \(S^{-1}AS = D\) forma la base teórica de la diagonalización.
Proceso Paso a Paso de Diagonalización de una Matriz
Paso 1 - Encontrar el Polinomio Característico
El primer paso para diagonalizar una matriz es calcular sus valores propios usando el polinomio característico:
\(p(t) = \text{det}(A - tI)\)
1. Construir \(A - tI\) restando \(t\) de las entradas diagonales de \(A\).
2. Calcular el determinante de \(A - tI\).
Ejemplo: Para \(A = \begin{bmatrix} 2 & 3 \\ 1 & 4 \end{bmatrix}\),
\(A - tI = \begin{bmatrix} 2 - t & 3 \\ 1 & 4 - t \end{bmatrix}\)
\(p(t) = \text{det}(A - tI) = (2 - t)(4 - t) - (3)(1) = t^2 - 6t + 5\)
Por lo tanto, los valores propios son \(t = 1\) y \(t = 5\).
Para matrices más grandes (por ejemplo, 3×3 o más), calcule el determinante utilizando la expansión por cofactores.
Paso 2 - Encontrar los Valores Propios
Resolver la ecuación característica \(p(t) = 0\) proporciona los valores propios \(\lambda_1, \lambda_2, \dots, \lambda_n\). Cada raíz corresponde a un valor propio.
- Errores comunes: Tenga cuidado en contabilizar con precisión múltiples raíces; los valores propios repetidos requieren atención tanto a las multiplicidades algebraicas como geométricas; por ejemplo, aunque aparezcan dos valores propios, solo uno puede contener un vector propio e indicar que la diagonalización no es una opción en su matriz.
Paso 3 - Calcular los Vectores Propios
Después de encontrar los valores propios, calcule los vectores propios correspondientes a cada valor propio. Los vectores propios \(x\) resuelven la ecuación:
\((A - \lambda I)x = 0\)
Para cada valor propio \(\lambda\):
1. Sustituya \(\lambda\) en \(A - \lambda I\).
2. Resuelva el sistema homogéneo \((A - \lambda I)x = 0\) utilizando la reducción por filas para obtener el espacio nulo de \(A - \lambda I\).
Ejemplo:
Para \(A = \begin{bmatrix} 2 & 3 \\ 1 & 4 \end{bmatrix}\) y valor propio \(\lambda = 1\):
\(A - 1I = \begin{bmatrix} 1 & 3 \\ 1 & 3 \end{bmatrix}\)
Reducción por filas de \(A - 1I\):
\(\begin{bmatrix} 1 & 3 \\ 0 & 0 \end{bmatrix}\)
La solución a la ecuación del vector propio es:
\(x = \begin{bmatrix} -3 \\ 1 \end{bmatrix}\)
Por lo tanto, \(v_1 = \begin{bmatrix} -3 \\ 1 \end{bmatrix}\) es un vector propio para \(\lambda = 1\).
Valores Propios Múltiples:
Si \(\lambda = 5\), repita el proceso anterior para este valor propio. Al considerar valores propios con multiplicidades algebraicas mayores a uno, debe asegurarse de identificar el conjunto completo de vectores propios linealmente independientes. Siempre que solo se encuentren algunos, esto indica que la multiplicidad geométrica supera a la multiplicidad algebraica y debe abordarse de inmediato, ya que esto indica un defecto de matriz y requiere una investigación adicional.
Paso 4 - Comprobar Si la Matriz es Diagonalizable
Para confirmar si una matriz es diagonalizable:
1. Verifique si el número total de vectores propios linealmente independientes es igual al tamaño de la matriz (n×n significa que se requieren n vectores propios).
2. Asegúrese de que la multiplicidad geométrica (dimensión del espacio propio) para cada valor propio coincida con su multiplicidad algebraica (raíces repetidas de polinomios característicos).
Una matriz no diagonalizable se refiere como defectuosa. Por ejemplo, una matriz con el valor propio \(\lambda = 2\) (multiplicidad algebraica 2) pero solo un vector propio linealmente independiente es defectuosa.
Consejo Práctico: Visualice los espacios propios como diferentes "direcciones" que los vectores propios abarcan. Todas estas direcciones deben combinarse para llenar todo el espacio para que la matriz sea diagonalizable.
Paso 5 - Construir las Matrices \(S\) y \(D\)
Una vez que se han calculado los vectores propios:
1. Construya \(S\), la matriz cuyas columnas son los vectores propios de \(A\).
El orden de los vectores propios determina la disposición de los correspondientes valores propios en \(D\).
- \(S = [v_1 \, v_2 \, \dots \, v_n]\).
2. Construya \(D\), la matriz diagonal donde los valores propios aparecen a lo largo de la diagonal.
\(D = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)\)
Ejemplo:
Para los vectores propios \(v_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\), \(v_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) y los valores propios \(\lambda_1 = 1\), \(\lambda_2 = 5\):
\(S = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \; D = \begin{bmatrix} 1 & 0 \\ 0 & 5 \end{bmatrix}\)
\(H3: Opcional: Calcular \( S^{-1} \)\)
Para completar la fórmula de diagonalización:
\(S^{-1}AS = D\)
Calcule \(S^{-1}\), la inversa de \(S\):
1. Use la reducción por filas (eliminación Gauss-Jordan) para calcular \(S^{-1}\): Anexe \(I\) a \(S\), y transforme \(S\) en \(I\), mientras \(I\) se convierte en Aplicaciones de la Diagonalización Un beneficio principal de la diagonalización es la capacidad de simplificar las operaciones de matrices, particularmente las potencias de matrices. Suponga que \(A\) es diagonalizable, entonces: \(A^n = S D^n S^{-1}\) Elevar una matriz diagonal \(D\) a la potencia \(n\)-ésima es sencillo ya que: \(D^n = \text{diag}(\lambda_1^n, \lambda_2^n, \dots, \lambda_n^n)\) Ejemplo: Para \(A = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}\), \(D = A\): \(A^5 = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}^5 = \begin{bmatrix} 2^5 & 0 \\ 0 & 3^5 \end{bmatrix} = \begin{bmatrix} 32 & 0 \\ 0 & 243 \end{bmatrix}\) Esta característica es notablemente ventajosa para examinar patrones de comportamiento sostenidos en poblaciones ecológicas o construir simulaciones de sistemas mecánicos. La diagonalización es una herramienta poderosa para resolver sistemas de ecuaciones diferenciales lineales. Los sistemas expresados como \(\dot{x} = Ax\), donde \(x\) es un vector y \(A\) es una matriz de coeficientes, pueden simplificarse usando diagonalización: 1. Suponga que \(A = S D S^{-1}\). Escriba \(\dot{x} = S D S^{-1}x\). 2. Sustituya \(y = S^{-1}x\): \(\dot{y} = D y\). 3. Resuelva el sistema desacoplado \(\dot{y}_i = \lambda_i y_i\) para cada \(y_i\). 4. Transforme de nuevo: \(x = S y\). En física, la diagonalización se utiliza en mecánica cuántica para desacoplar ecuaciones de Schrödinger, permitiendo soluciones para estados de energía independientes. Aunque la diagonalización es muy útil, no todas las matrices pueden ser diagonalizadas. Para matrices defectuosas, aquellas que carecen de suficientes vectores propios linealmente independientes, el concepto de Forma Normal de Jordan (o Forma Canónica de Jordan) ofrece una alternativa. En lugar de generar una matriz diagonal, la transformación produce una disposición en bloque-diagonal en la que los bloques individuales se asocian con valores propios pero pueden incorporar entradas acopladas denominadas bloques de Jordan. Ejemplo: Para una matriz defectuosa \(A = \begin{bmatrix} 5 & 1 \\ 0 & 5 \end{bmatrix}\) con valor propio \(\lambda = 5\) de multiplicidad algebraica 2 pero multiplicidad geométrica 1, la diagonalización no es posible. Sin embargo, la Forma Normal de Jordan es: \(J = \begin{bmatrix} 5 & 1 \\ 0 & 5 \end{bmatrix}\) La Forma de Jordan nos permite trabajar con matrices para aplicaciones que requieren potencias de matrices o resolver ecuaciones diferenciales. Aunque es ligeramente más compleja que la diagonalización, la Forma de Jordan asegura que el análisis de matrices siga siendo factible aún en casos desafiantes. La diagonalización juega un papel crucial en el Análisis de Componentes Principales (PCA, por sus siglas en inglés), una técnica de reducción de dimensionalidad utilizada para simplificar conjuntos de datos con muchas variables. En PCA: 1. Se calcula la matriz de covarianza \(\Sigma\) de los datos. 2. Se determinan los valores propios y vectores propios de \(\Sigma\). 3. Los vectores propios definen nuevas "ejes principales" (direcciones de máxima varianza), y sus valores propios correspondientes indican el nivel de varianza capturada. Ejemplo: En el procesamiento de imágenes, la diagonalización se utiliza para comprimir imágenes de alta dimensión proyectándolas en los componentes principales de top-k. Esto reduce esencialmente los requisitos de almacenamiento mientras se preservan características críticas. Por ejemplo, la descomposición en valores propios puede simplificar conjuntos de datos de reconocimiento facial de alta dimensión, mejorando la eficiencia computacional en el aprendizaje automático. ¿Qué sucede si todos los valores propios son números complejos? Los valores propios complejos a menudo surgen en matrices reales para transformaciones de rotación u oscilatorias. Aunque tales matrices no pueden ser diagonalizadas sobre números reales, los números complejos permiten su diagonalización. ¿Todas las matrices pueden ser diagonalizadas? No. Para ser diagonalizada, una matriz debe contener suficientes vectores propios linealmente independientes que sean linealmente independientes entre sí y suficiente multiplicidad lineal para que su multiplicidad algebraica sobrepase la multiplicidad geométrica; cualquier matriz defectuosa no puede ser diagonalizada debido a que la multiplicidad geométrica es menor que la multiplicidad algebraica. - Desajustar vectores propios y valores propios: Asegúrese de que cada valor propio corresponda a su vector propio al construir matrices \(S\) y \(D\). - Pasar por alto las comprobaciones de multiplicidad: Siempre verifique que la multiplicidad geométrica coincida con la multiplicidad algebraica para todos los valores propios. - Errores de cálculo de la inversa: Al calcular \(S^{-1}\), los errores numéricos, especialmente para matrices mal condicionadas, pueden llevar a resultados incorrectos. Verifique los resultados para asegurar que la multiplicación sea consistente \(S \cdot S^{-1} = I\). La diagonalización es un proceso transformador que simplifica los cálculos de matrices. Los pasos incluyen: 1. Encontrar el polinomio característico y resolver para los valores propios. 2. Calcular los vectores propios y verificar las multiplicidades geométrica y algebraica. 3. Construir las matrices \(S\) (vectores propios) y \(D\) (valores propios en la diagonal). La diagonalización permite que operaciones complejas como potencias de matrices o resolver ecuaciones diferenciales se transformen en tareas más simples y computacionalmente eficientes mediante la diagonalización. La diagonalización de matrices es uno de los pilares del álgebra lineal y encuentra aplicaciones en física, ingeniería y aprendizaje automático. Al dominar este concepto, desbloqueará el poder de analizar conjuntos de datos, resolver sistemas dinámicos y optimizar cálculos. Para temas avanzados, pruebe la Forma Normal de Jordan o métodos numéricos para diagonalizar matrices grandes, como los entornos de programación de Python o MATLAB. Referencia: https://textbooks.math.gatech.edu/ila/characteristic-polynomial.html https://builtin.com/data-science/step-step-explanation-principal-component-analysisSimplificación de Cálculos de Matrices
Resolución de Sistemas de Ecuaciones Diferenciales Lineales
Más allá de lo Básico: Perspectivas No Tradicionales sobre Diagonalización
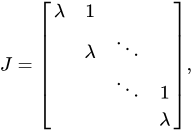
Matrices No Diagonalizables y "Forma Normal de Jordan"
Conexión con el Aprendizaje Automático y la Ciencia de Datos
Preguntas Frecuentes y Errores Comunes
Preguntas Frecuentes
Errores a Evitar Durante la Diagonalización
Conclusión