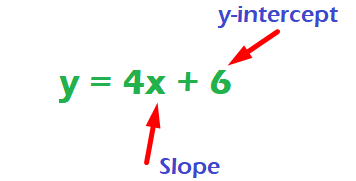Cómo encontrar la ecuación de una recta

¿Qué es una ecuación lineal?

Definición y Componentes

Definición & Estructura

Una ecuación lineal es una representación matemática de una relación lineal entre dos variables. Generalmente se expresa como y = mx + c.

m representa la pendiente, que es la medida de la inclinación o inclinación de la línea. Un valor más alto de m indica una línea más empinada.

C indica la intersección con el eje y, el punto en el cual una línea cruza su respectivo eje y y marca donde comienza su posición inicial respecto a y. Juntos, m y c proporcionan un formato fácilmente comprensible y altamente aplicable que describe todos los aspectos de la geometría de líneas rectas.

Aplicabilidad

Las ecuaciones lineales juegan un papel esencial en el modelado matemático, pronósticos financieros, diseño de ingeniería y ciencias sociales - desde el modelado de presupuestos proporcional a las cantidades de producción hasta el seguimiento de la velocidad en el tiempo en sistemas físicos - usar ecuaciones lineales proporciona un medio simple pero poderoso de caracterizar sus comportamientos. Por ejemplo, los gastos proporcionales a cantidades de producción o la velocidad en el tiempo en sistemas físicos pueden ser representados mediante estas expresiones matemáticas simples pero efectivas.

Reordenación de Ecuaciones

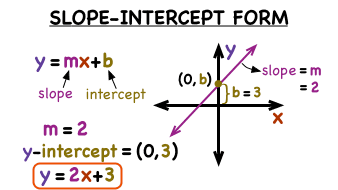
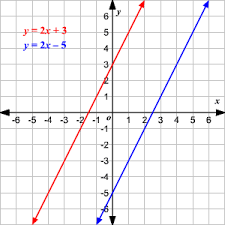
No todas las ecuaciones pueden ser representadas usando la forma de intersección-slope (y=mx+c). Considera, por ejemplo, ecuaciones como 2y-4x=6, que deben ser modificadas para aislar y. En este caso:

2y−4x=6⟹y=2x+3.

Reordenar simplifica la estructura de una ecuación y hace que su pendiente (m=2) y su intersección con y (c=3) sean fáciles de identificar mientras simplifica la graficación e interpretación de su relación entre variables.

Forma Pendiente-Intersección

Definición y Concepto de la Forma Pendiente-Intersección

Estructura Básica

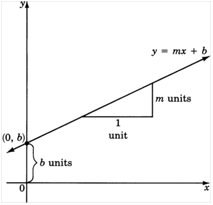
La forma pendiente-intersección (y=mx+c) es un formato establecido para ecuaciones lineales. La pendiente (m) define qué tan empinadamente o suavemente sube o baja una línea; por ejemplo, un incremento de una unidad en x causará un incremento igual en y. Por ejemplo, cuando se establece en cinco, esto significa que por cada aumento de 1 unidad de x, un incremento de cinco unidades causará que y aumente simultáneamente.
La intersección con el eje y (c) define dónde una línea cruza el eje y y se ancla en su gráfico en x=0. No solo esta forma es visualmente intuitiva, sino que permite cálculos rápidos cuando se proporcionan valores de pendiente e intersección con el eje y.

Aplicación Directa

Cuando la pendiente m y la intersección con el eje y c son conocidas, crear una ecuación lineal se convierte en un proceso simple de enchufar y usar. Por ejemplo, si una empresa de alquiler de autos cobra una tarifa base de 50 (c) y 0.20 por milla (m), la ecuación del costo total es y=0.2x+50, donde x representa las millas conducidas.

Pasos para Resolver

Paso 1

Identificar la pendiente (m) y la intersección con el eje y (c). A menudo, estos valores se proporcionan directamente en el problema.

Paso 2

Sustituir la pendiente e intersección identificadas en y=mx+c.
Por ejemplo, dado m=−3 y c=6, la ecuación resultante es:

y=−3x+6.

Método Rápido de Validación

Prueba la ecuación sustituyendo un punto conocido. Para el ejemplo anterior (y=−3x+6), sustituye x=2:

y=−3(2)+6=0.

Cuando esto coincide con el valor esperado, significa que la ecuación ha sido correctamente predicha y aplicada. Este método proporciona una capa adicional de confianza, particularmente útil en exámenes o escenarios de resolución de problemas donde la precisión es importante.

Forma Pendiente-Punto

Definición y Concepto de la Forma Pendiente-Punto

Fórmula General

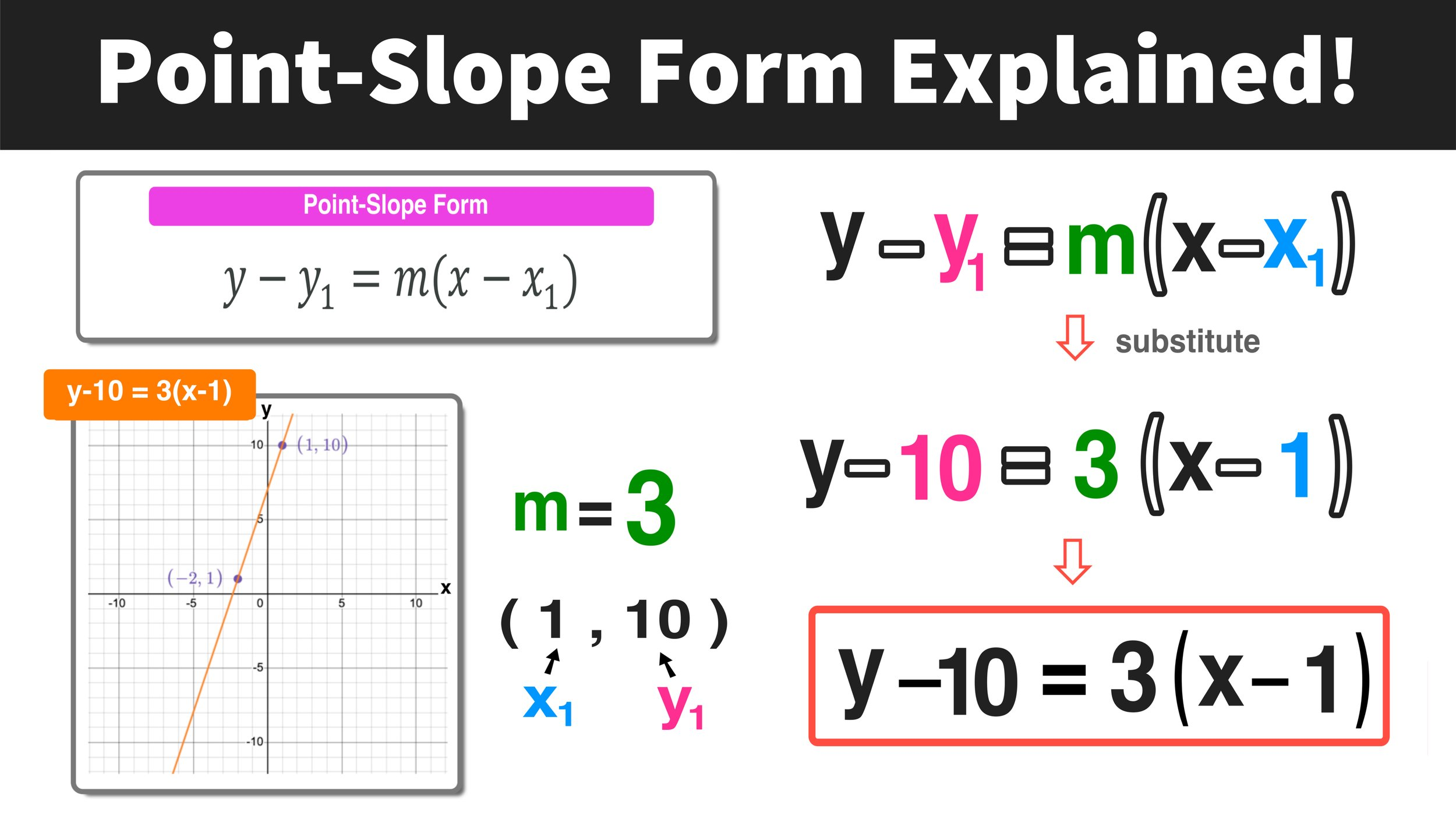
La forma pendiente-punto de una ecuación lineal se expresa como:

\(y−y_{1}​=m(x−x_{1}​)\),

donde m representa la pendiente, y (\(x_{1} ​,y_{1}\)) denota un punto en la línea. Esta forma es ideal para situaciones donde se te proporciona la pendiente y al menos un punto específico pero careces de la intersección en y.

Pasos para Resolver

Paso 1

Calcula o identifica la pendiente (m). Esto podría requerir usar la fórmula para la pendiente si no se proporciona directamente:

\(m= \frac{y_{2} -y_{1} }{x_{2} -x_{1}} ​​.\)

Paso 2

Selecciona un punto conocido (\(x_{1}​,y_{1}​\)) del contexto del problema.

Paso 3

Sustituye la pendiente y el punto en la fórmula. Por ejemplo, usando m=4 y el punto (1,3):

y−3=4(x−1).

Paso 4

Simplifica a forma pendiente-intersección (y=mx+c), si es necesario. Expandiendo el ejemplo anterior:

y−3=4x−4⟹y=4x−1.

Validación con Geometría

Prueba visualmente la precisión de una ecuación graficando su punto dado y trazando su pendiente; por ejemplo, al graficar (1,3) a lo largo de una pendiente de 4 se creará una línea consistente con su ecuación y=4x-1; este enfoque de dos pasos refuerza simultáneamente tanto la comprensión como la precisión.

Por Qué Las Líneas Paralelas y Perpendiculares Son Especiales

Propiedades de las Líneas Paralelas

Definición y Característica Clave

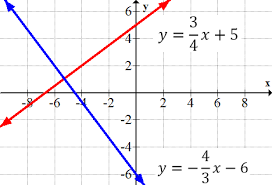
Las líneas paralelas comparten la misma pendiente (\(m_{1}​=m_{2}​\)) pero tienen distintas intersecciones con el eje y. Esto significa que nunca se intersectan y mantienen una distancia constante en el gráfico.

Pasos para Resolver Ecuaciones de Líneas Paralelas

Identifica la pendiente (m) de la línea dada.

Usa la misma pendiente con el nuevo punto proporcionado para la línea paralela en la forma de punto-pendiente.

Por ejemplo, si la línea y=3x+2 es paralela a otra línea que pasa por el punto (4,10):

y−10=3(x−4)⟹y=3x−2

Propiedades de las Líneas Perpendiculares

Relación de Recíproco Negativo

Si dos líneas son perpendiculares, sus pendientes multiplicadas dan como resultado −1. Por ejemplo, si una pendiente es m=2, la pendiente perpendicular es \(m=−\frac{1}{2}\).

Ejemplo de Problema

Dada la línea \(y=\frac{1}{3} ​x+2\), encuentra la línea perpendicular que pasa por el punto (6,−1):

m=−3, entonces y+1=−3(x−6)⟹y=−3x+17.

Comprensión a Través de la Simetría

El concepto de simetría ofrece una forma clara de entender las líneas perpendiculares. Visualiza la línea original como un eje de espejo en un gráfico, con la línea perpendicular cruzándola en un ángulo de 90 grados, lo que proporciona una manera intuitiva de comprender su relación. Las pendientes de estas líneas que son recíprocos negativos crean un equilibrio cuando se balancean simétricamente; por ejemplo, si una línea tiene una pendiente hacia arriba \(m_{1}=2\), otra seguiría y tendría una pendiente en dirección opuesta de \(m_{2} =-\frac{1}{2}\); de esta manera creamos un diseño equilibrado. Cuando dos líneas se encuentran en un gráfico, su intersección formará ángulos rectos consistentes, que visualmente la dividen en cuatro cuadrantes iguales. El trazado resalta aún más esta simetría: cada subida y bajada de una línea se refleja en su contraparte para añadir perpendicularidad durante los cálculos de pendiente y los propósitos de alineación espacial.

Aplicaciones del Mundo Real

Uso Práctico

Las ecuaciones lineales han sido durante mucho tiempo utilizadas por las empresas como una forma invaluable de modelar relaciones cuantitativas en diversas industrias. Las empresas las utilizan para pronosticar la demanda, establecer estrategias de precios y estimar la rentabilidad; un ejemplo es el uso de ecuaciones de ingresos como 40x+200 para pronosticar la demanda o estimar la rentabilidad a partir de los datos de volumen de ventas. Las ecuaciones lineales también modelan los costos de transporte por milla para optimizar el uso de combustible y mano de obra, mejorando la precisión de los precios y la toma de decisiones en empresas de logística o incluso minoristas en línea que utilizan cálculos de envío basados en la distancia o el peso al enviar paquetes; todo esto ilustra cómo las ecuaciones lineales transforman los datos en ideas accionables y estrategias empresariales informadas.

Planificación y Optimización

Las ecuaciones lineales juegan un papel central en la planificación de recursos y la optimización de costos en industrias como la manufactura, las cadenas de suministro y el presupuesto de proyectos. Modelos como 50x+500 (donde x es la producción, 50 es el costo variable por unidad, y 500 son los costos fijos respectivamente) ayudan a determinar niveles de producción rentables mientras se optimizan las cadenas de suministro mediante la minimización de costos de transporte con horarios de entrega para minimizar gastos. Los gerentes de proyectos emplean ecuaciones lineales para pronosticar gastos desglosando costos como tarifas laborales por hora de los fijos como el alquiler de equipos para crear modelos claros; herramientas que permiten a las empresas simular resultados y maximizar eficiencias, mientras toman decisiones financieras informadas y planean y presupuestan en consecuencia.

Usando Gráficas para Encontrar Ecuaciones Lineales

Las gráficas son un medio visual e intuitivo para analizar las relaciones entre variables. Al trabajar con ecuaciones lineales, las gráficas proporcionan un excelente medio para derivar componentes clave tales como pendiente y la intersección con el eje y directamente. Esta sección enfatiza tanto el análisis manual de gráficas para datos ideales como los métodos computacionales para datos irregulares o dispersos.

Identificando Pendiente e Intersección de una Gráfica

Extraer Datos

Para determinar la ecuación de una línea a partir de una gráfica:

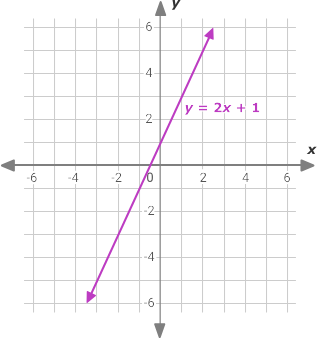
1. Identificar su ecuación desde su línea graficada: Marcar al menos dos puntos claramente identificables en su línea que se encuentren cerca de las intersecciones de la cuadrícula para facilitar el cálculo y reducir errores; ejemplos podrían incluir (1,3) y (4,9) ya que estos puntos podrían funcionar bien como puntos de inicio.

2. Utilizar estos dos puntos para calcular la pendiente (m), que es la razón del cambio vertical (\(\bigtriangleup y\)) al cambio horizontal (\(\bigtriangleup x\)):

\(\frac{\bigtriangleup y }{\bigtriangleup x} =\frac{9-3}{4-1} =\frac{6}{3} =2\)

3. Observar dónde la línea interseca el eje y para determinar la intersección con el eje y (c). Por ejemplo, supongamos que la gráfica cruza el eje y en (0,1), lo que hace c=1.

Combinar Componentes

Ahora, sustituir estos valores en la forma pendiente-intersección y=mx+c. La ecuación resultante es:

y=2x+1.

Tratando con Datos Irregulares

Líneas de Tendencia para Datos Dispersos

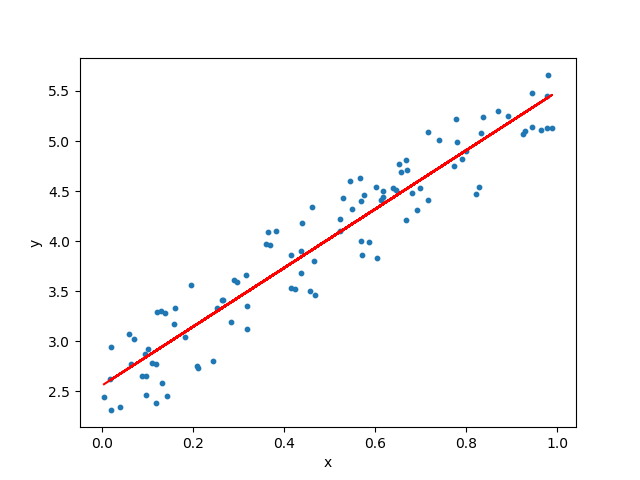
Las aplicaciones del mundo real involucran datos ruidosos. Una gráfica suele ser desordenada, con puntos dispersos en lugar de caer perfectamente a lo largo de una línea recta. Para derivar relaciones lineales significativas:

Aproximación mediante Líneas de Tendencia : Dibujar una línea de tendencia que mejor coincida con la distribución de puntos, representando su comportamiento promedio como datos y ayudándote a estimar pendiente e intersección.

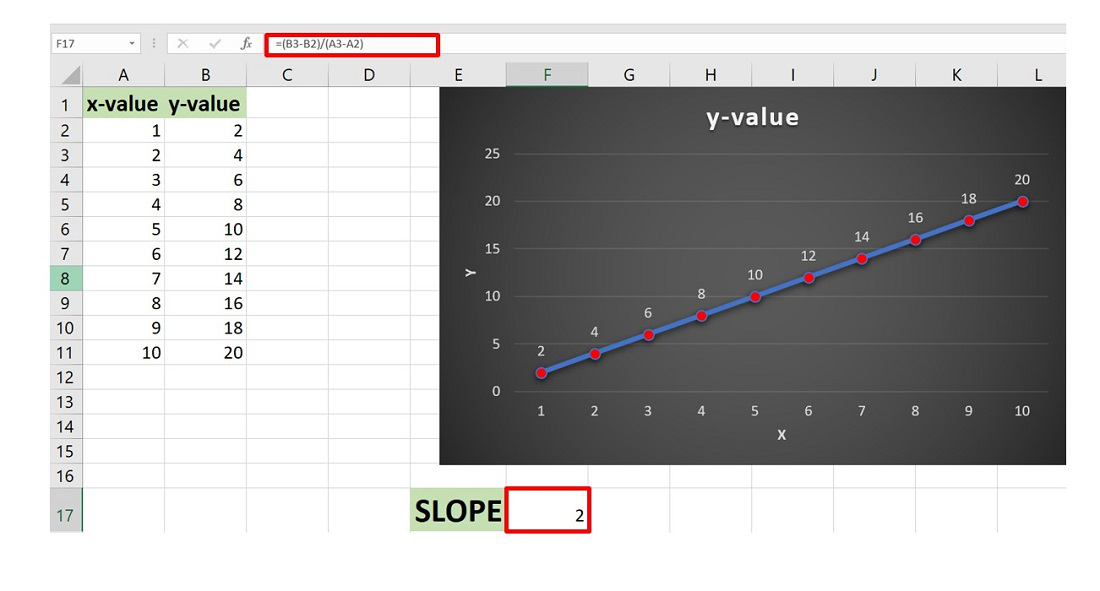
Soporte Computacional : Utilizar software como Excel, Google Sheets o bibliotecas de Python para construir la línea de mejor ajuste usando regresión lineal. Dichas herramientas estiman pendiente (m) e intersección (c), minimizando los errores entre los puntos reales y los valores predichos.

Al proporcionar estrategias que abordan tanto las líneas gráficas ideales como los puntos de datos irregulares, este enfoque te equipa para abordar varias ecuaciones lineales derivadas de gráficas.

Errores Comunes y Cómo Evitarlos

Los errores al resolver o interpretar ecuaciones lineales son comunes, pero se pueden evitar con atención cuidadosa a los detalles y un enfoque metódico para resolver problemas.

Confusión Entre Pendiente e Intersección

Problema

Un error frecuente es confundir la pendiente (m) con la intersección en el eje y (c). Muchos confunden el coeficiente de x (m) como la intersección o viceversa. Esto ocurre porque no logran distinguir entre las funciones de estos dos elementos:

La pendiente (m) describe la inclinación de la línea y la tasa de cambio.

La intersección en el eje y (c) determina dónde la línea cruza el eje y en x=0.

Solución

Siempre relaciona cada término con su significado geométrico en el gráfico mientras trabajas. Practicar visualizaciones basadas en gráficos puede solidificar estos conceptos.

Error en los Signos de Coordenadas

Problema

Los errores suelen ocurrir al manejar coordenadas positivas y negativas, especialmente si una dimensión (por ejemplo, x o y) involucra valores negativos. Por ejemplo, al realizar cálculos como \(\bigtriangleup y=y_{2}-y_{1}\)​, olvidar el signo negativo de un valor de y invalida por completo el cálculo.

Solución

Revisa todas las coordenadas antes de calcular la pendiente o la intersección y escribe explícitamente cada signo durante los cálculos.

Malinterpretación de \(\bigtriangleup x\) o \(\bigtriangleup y\)

Problema

Interpretar incorrectamente la escala del gráfico puede llevar a errores al calcular el cambio en x (\(\bigtriangleup x\)) o y (\(\bigtriangleup y\)). Por ejemplo, asumir que un incremento de cuadrícula representa 1 en lugar de 0.5 podría resultar en un error de pendiente.

Solución

Examina cuidadosamente las etiquetas de los ejes del gráfico y utiliza medidas precisas al determinar la elevación sobre el recorrido.

Aplicaciones avanzadas y herramientas

Las ecuaciones lineales proporcionan una puerta de entrada a un nivel más avanzado de resolución de problemas matemáticos. El aprovechamiento de la tecnología y la extensión de conceptos más allá de las relaciones de una sola variable permiten un análisis y una comprensión más amplios.

Ecuaciones lineales multivariable

Mientras que las ecuaciones lineales básicas involucran solo dos variables (x e y), muchos sistemas necesitan múltiples variables para modelar con precisión situaciones complejas, incluyendo:
La previsión de beneficios requiere tener en cuenta la mano de obra (\(x_{1}\)), el material (\(x_{2}\)) y los costos generales (\(x_{3}\)) al predecir beneficios; el resultado podría verse algo así:\(y=50x_{1} +40x_{2} ​+100x_{3} ​+500\). Este enfoque ayuda a las empresas e investigadores a analizar múltiples factores influyentes simultáneamente.

Aprovechando el software para cálculos

Las herramientas modernas simplifican la regresión lineal, el análisis de datos y la trazado de gráficos. Por ejemplo:

Excel o Google Sheets

Las funciones integradas como LINEST se utilizan para derivar valores de pendiente e intercepto a partir de puntos de datos.

Python con Matplotlib o NumPy

Trazar datos eficientemente, calcular líneas de mejor ajuste rápidamente, y visualizar ecuaciones fácilmente usando un script en Python. Un script puede analizar cientos de puntos de datos rápidamente para conjuntos de datos grandes, ideal para exploraciones rápidas pero precisas de comportamientos lineales mientras se eliminan errores manuales.

Conclusión

Las ecuaciones lineales son herramientas prácticas que unen la teoría matemática con aplicaciones del mundo real. Dominando métodos como la forma pendiente-intercepto, la forma punto-pendiente y el método de los dos puntos, puedes resolver efectivamente una amplia gama de problemas. Estas ecuaciones ayudan a modelar relaciones, predecir tendencias y optimizar decisiones en diversas industrias, desde la ciencia hasta los negocios.

Entender los conceptos lineales, ya sea a través de la representación gráfica, trabajar con líneas paralelas y perpendiculares, o aplicar herramientas computacionales, proporciona habilidades valiosas para el crecimiento académico y profesional. A medida que continúes explorando, las ecuaciones lineales servirán como una base confiable para abordar desafíos más complejos e interpretar datos del mundo real con precisión.

Referencia：

https://www.simplilearn.com/tutorials/excel-tutorial/data-analysis-excel

https://www.mdpi.com/2078-2489/11/4/193

https://www.statology.org/predictions-regression/