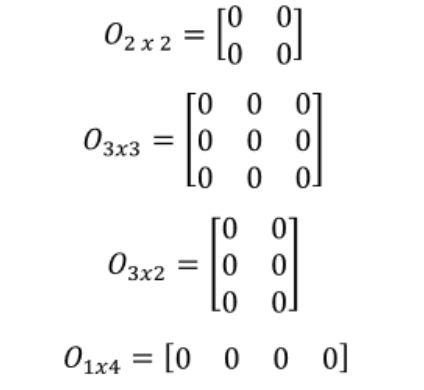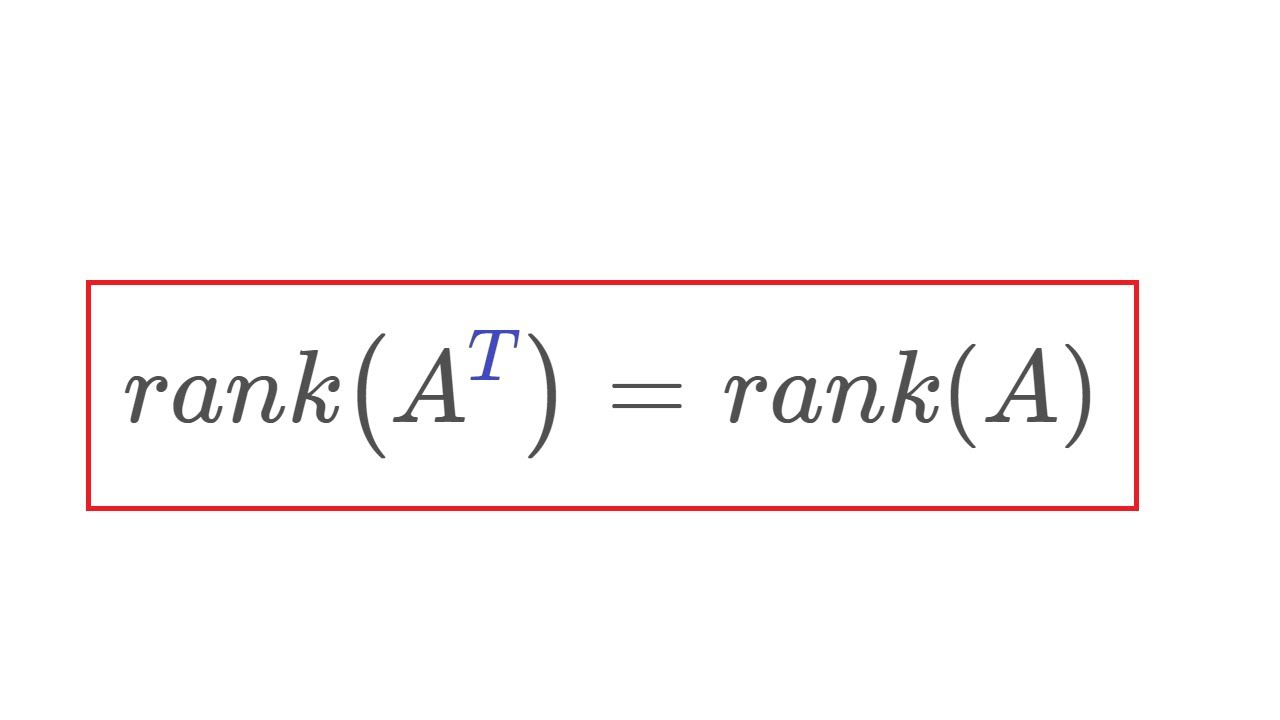¿Cómo encontrar el rango de una matriz?
Aprende métodos paso a paso para encontrar el rango de una matriz, incluyendo la forma escalonada por filas, menores y la descomposición en valores singulares (SVD). ¡Entiende su importancia en la resolución de problemas del mundo real!
Alice Brooks
Feb 8, 2025 12 minutos leer
Introducción al Rango de una Matriz
¿Qué es el Rango de una Matriz?
En álgebra lineal, el rango es un concepto esencial que mide la dimensión del espacio vectorial generado por sus filas o columnas. Dicho de manera más simple, el rango muestra cuánta "información" o cuántas filas o columnas independientes tiene una matriz. Por ejemplo, considere una matriz \(A\) que tiene filas o columnas que pueden escribirse como combinaciones lineales de otras. El rango refleja el número de filas o columnas verdaderamente esenciales e independientes.
Matemáticamente, el rango de una matriz puede definirse de la siguiente manera:
1. Máximo número de filas linealmente independientes (rango de fila).
2. Máximo número de columnas linealmente independientes (rango de columna).
Un teorema clave en álgebra lineal establece que el rango de filas y el rango de columnas siempre suman uno; cuando se toman juntos, forman lo que se conoce como rango de la matriz.
Ejemplo:
Si la matriz \(A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\), el rango de fila se determina evaluando cuántas filas son linealmente independientes, y de manera similar, se verifica el rango de columna para la independencia lineal entre las columnas. Exploraremos cómo calcular esto con detalle más adelante.
¿Por qué es Importante el Rango en Álgebra Lineal?
El rango de una matriz juega un papel significativo en la teoría de sistemas lineales de ecuaciones, transformaciones y sus aplicaciones a través de diversas áreas como estadística, informática e ingeniería. Intuitivamente, una matriz con rango deficiente (donde no todas las filas o columnas son independientes) carece de "información completa" o "dimensión completa", lo cual puede restringir su uso.
Aquí hay algunas razones por las que el rango es crucial:
1. Resolución de Sistemas Lineales:
El rango determina si un sistema de ecuaciones contiene una solución única o infinitas soluciones, dependiendo de si existe solo una solución única o infinitas para ellas.
2. Representación Dimensional:Rango puede proporcionar una visión sobre la dimensión real de los espacios vectoriales de fila y columna - este conocimiento es crucial tanto en álgebra lineal teórica como aplicada.
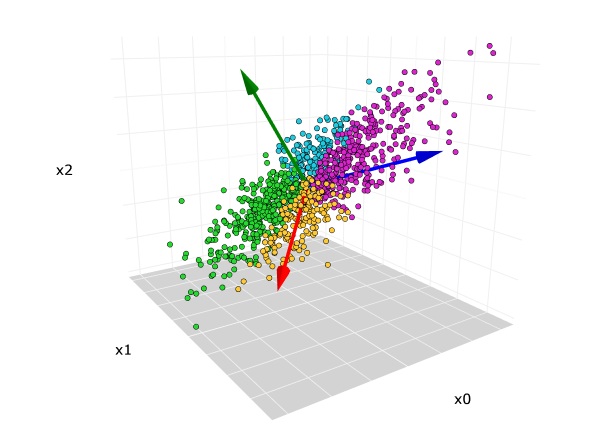
3. Aplicaciones en Aprendizaje Automático y Ciencia de Datos: Para aplicaciones como el análisis de componentes principales (PCA) y la descomposición en valores singulares (SVD), el rango de la matriz juega un papel instrumental en la comprensión y simplificación de conjuntos de datos.
4. Comprensión de Transformaciones: En geometría, las matrices representan transformaciones lineales de espacios vectoriales. Su rango proporciona información sobre si comprimen dimensiones o las preservan durante las transformaciones.
El rango de una matriz puede servir tanto a necesidades teóricas como prácticas para comprender los datos estructurados y las transformaciones.
Propiedades Clave del Rango de una Matriz
Propiedades Fundamentales del Rango de una Matriz
Entender las propiedades del rango es esencial antes de profundizar en los métodos para calcularlo. Aquí hay algunas propiedades fundamentales y sus implicaciones.
Igualdad de Rango de Filas y Columnas
Como se mencionó anteriormente, el rango de una matriz es tanto el rango de filas como el de columnas y estos dos siempre son iguales. Este es un resultado central en álgebra lineal.
- Ejemplo: Para \(A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\), el rango de filas y el rango de columnas son ambos 2.
Rango de una Matriz Cero
Una matriz cero no contiene vectores fila o columna no nulos. Por lo tanto, el rango de una \(m \times n\) matriz cero es siempre 0.
\(A = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\) tiene rango 0.
Rango y Transposición de Matrices
El rango de una matriz permanece sin cambios bajo transposición. Es decir, \(\text{rank}(A) = \text{rank}(A^T)\).
Rango de un Producto
Si \(A\) es \(m \times n\) y \(B\) es \(n \times p\), \(\text{rank}(AB) \leq \min (\text{rank}(A), \text{rank}(B))\).
Adición de Matrices y Rango
En general, \(\text{rank}(A + B) \leq \text{rank}(A) + \text{rank}(B)\).
Rango de una Matriz Identidad
El rango de una matriz identidad \(I_n\) es \(n\), ya que todas las filas (o columnas) de \(I_n\) son linealmente independientes.
Matrices Especiales y Sus Rangos
Matriz Diagonal
Para una matriz diagonal, el rango es simplemente el número de elementos diagonales no nulos.
Matrices Triangulares Superiores o Inferiores
Similar a las matrices diagonales, el rango es igual al número de filas o columnas no nulas.
Matriz Simétrica
Dado que las matrices simétricas satisfacen \(A = A^T\), su rango es invariante bajo transposición.
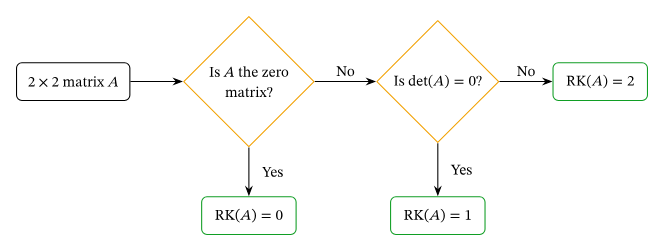
Matrices Singulares vs. No Singulares
Una matriz cuadrada es singular si \(\text{det}(A) = 0\), lo que implica que tiene deficiencia de rango. Por el contrario, una matriz no singular tiene un rango igual a su tamaño.
Métodos para Encontrar el Rango de una Matriz
Método 1: Usando el Método de Menores
Proceso Paso a Paso
El método de menores implica encontrar determinantes de todas las posibles submatrices cuadradas de una matriz. El tamaño más grande \(n\) para el cual un menor de \(n \times n\) tiene un determinante distinto de cero da el rango de la matriz.
1. Identifica y extrae todas las submatrices de la matriz dada \(A\).
2. Calcula el determinante para cada submatriz cuadrada.
3. El rango es el tamaño de la submatriz cuadrada más grande cuyo determinante no es cero.
Fortalezas y Limitaciones
- Fortalezas:
El método es altamente sistemático y adecuado para matrices pequeñas donde las submatrices pueden ser calculadas manualmente.
- Limitaciones:
Se vuelve prohibitivo computacionalmente a medida que aumenta el tamaño de la matriz, dado el crecimiento exponencial en el número de submatrices.
Ejemplo
Encuentra el rango de \(A = \begin{bmatrix} 1 & 2 \\ 3 & 6 \end{bmatrix}\).
Paso 1: Determina todos los menores de \(2 \times 2\).
\(\text{det}(A) = \text{det}\begin{bmatrix} 1 & 2 \\ 3 & 6 \end{bmatrix} = (1)(6)-(3)(2) = 0\)
Paso 2: Revisa todos los menores de \(1 \times 1\). Existen determinantes diferentes de cero, por lo que el rango = 1.
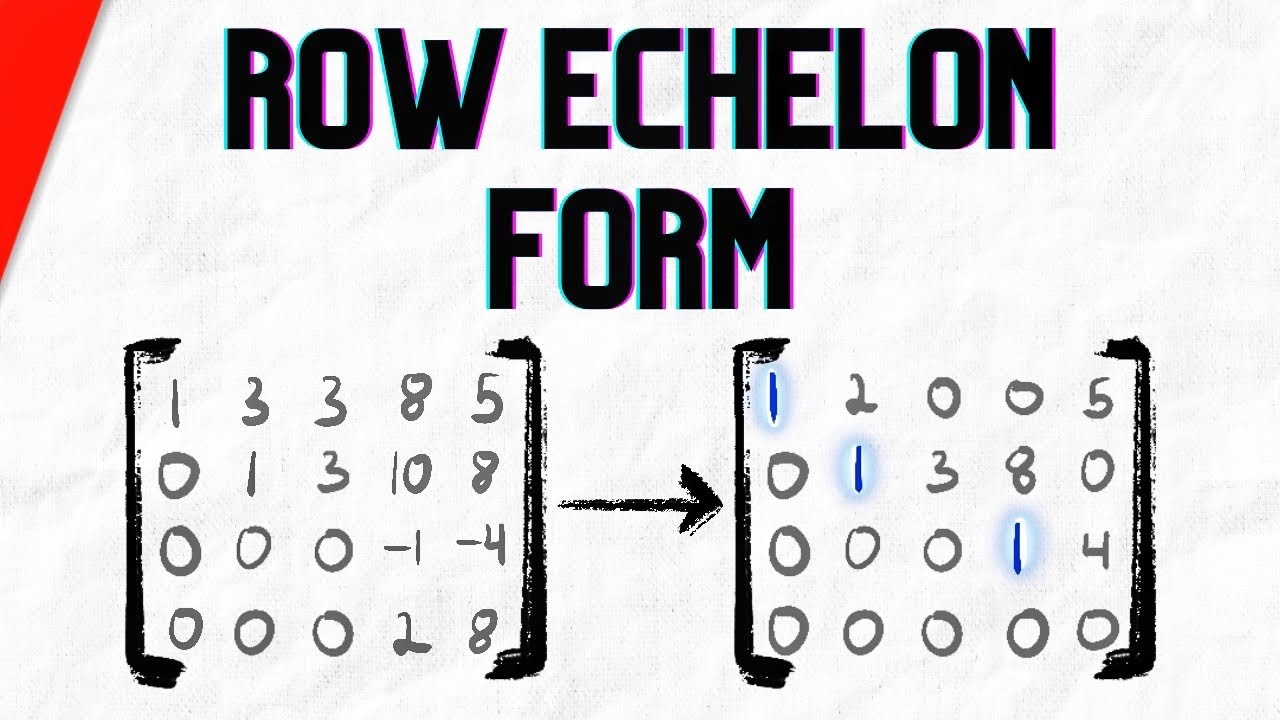
Método 2: Usando la Forma Escalonada de Fila
¿Qué es la Forma Escalonada?
Se dice que una matriz está en forma escalonada de fila si:
1. Todas las filas no nulas están por encima de las filas de ceros.
2. La entrada principal (también conocida como pivote) de cada fila no nula se encuentra a la derecha de la entrada principal en la fila inmediatamente superior.
3. Todos los elementos en una columna debajo de una entrada principal son cero.
Por ejemplo, esta matriz está en forma escalonada de fila:\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}\)
Proceso Paso a Paso
Para calcular el rango de una matriz usando REF:
1. Comienza con la matriz dada \(A\): Escribe la matriz inicial.
2. Aplica operaciones elementales de fila hasta que la matriz esté en forma escalonada de fila. Usa técnicas como escalar filas, intercambiar filas y sumar/restar filas para hacer cero los elementos por debajo de los pivotes.
3. Cuenta las filas no nulas: Una vez que la matriz esté en forma escalonada, el número de filas no nulas determina el rango de la matriz.
Transformaciones de Columna
Aunque las transformaciones de fila se utilizan con más frecuencia, las transformaciones de columna también pueden ser beneficiosas (aunque menos frecuentes). En lugar de solo considerar el rango de filas, al aplicar operaciones de columna como intercambiar columnas o sumar múltiplos de una columna a otra puede ayudar a llegar a la forma de triunfo de columna de la matriz, creando un equilibrio entre los análisis de fila y columna al mostrar que sus valores coinciden perfectamente, añadiendo un elemento equilibrador entre los análisis de filas versus columnas.
Ejemplo
Encuentra el rango de \(A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\).
Paso 1: Escribe la matriz.
\(A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\)
Paso 2: Realiza operaciones elementales de fila para obtener la REF:
- Resta 4*(Fila 1) de Fila 2:
\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & -3 & -6 \\ 7 & 8 & 9 \end{bmatrix}\)
- Resta 7*(Fila 1) de Fila 3:
\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & -3 & -6 \\ 0 & -6 & -12 \end{bmatrix}\)
- Divide Fila 2 por -3:
\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & -6 & -12 \end{bmatrix}\)
- Suma 6*(Fila 2) a Fila 3:
\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{bmatrix}\)
Paso 3: Cuenta las filas no nulas:
La matriz en forma escalonada de fila tiene dos filas no nulas. Por lo tanto, el rango de la matriz es 2.
Método 3: Usando la Forma Normal
¿Qué es la Forma Normal?
En álgebra lineal, la forma normal de una matriz (o forma canónica) se refiere a una matriz simplificada que es equivalente a la matriz original pero más fácil de analizar. Un método específico es la "forma escalonada de fila reducida" (RREF), que refina la REF.
En RREF, cada pivote es \(1\), y cada columna que contiene un pivote tiene ceros en todas las demás posiciones. Por ejemplo:
\(\begin{bmatrix} 1 & 0 & -5 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}\)
Proceso
1. Comienza con la matriz original.
2. Usa operaciones elementales de fila, como en el método REF, para simplificar la matriz.
3. Refina aún más las entradas de pivote para que cada pivote sea \(1\) y todas las demás entradas en la columna del pivote sean cero.
4. El rango sigue siendo el número de filas no nulas.
Ejemplo
Considera \(A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}\).
La matriz ya está en REF.
Para llevarla a RREF:
- Divide la Fila 1 por \(1\):
\(\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}\)
- Resta \(2 \times (\text{Fil})\)\(a 2)\) de Fila 1:
\(\begin{bmatrix} 1 & 0 & -5 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}\)
En RREF, hay dos filas no nulas. El rango es 2.
Método 4: Descomposición en Valores Singulares (SVD)
¿Qué es SVD?
La Descomposición en Valores Singulares es una técnica avanzada de álgebra lineal donde una matriz \(A\) se factoriza en tres matrices:
\(A = U \Sigma V^T\)
Aquí, \(U\) y \(V\) son matrices ortogonales, y \(\Sigma\) es una matriz diagonal que contiene los valores
Comparando los Métodos
Método de Menores vs. Forma de Escalón
- Ventajas del Método de Menores: Preciso para matrices pequeñas; garantiza el rango correcto basado en cálculos de determinantes.
- Desventajas: Complejidad computacional para matrices más grandes.
- Ventajas de la Forma de Escalón: Sistemático y escalable a dimensiones más grandes; más fácil de ejecutar manualmente o programáticamente.
- Desventajas: Requiere maestría de las operaciones con filas.
Forma de Escalón vs. Forma Normal
- Forma de Escalón: Más fácil de calcular y suficiente para la mayoría de los propósitos.
- Forma Normal (RREF): Refina los resultados aún más, lo cual es especialmente útil para verificar la independencia lineal.
SVD y Cuándo Usar Técnicas Avanzadas
SVD es excesivo para matrices simples pero inigualable para sistemas grandes y complejos donde las matrices tienen deficiencia de rango o están cerca de ser singulares. Use SVD para aplicaciones que involucren ruido, aproximaciones o alta precisión.
Aplicaciones Avanzadas del Rango de Matrices
Aplicaciones del Mundo Real del Rango de Matrices
Aprendizaje Automático
El Análisis de Componentes Principales (PCA), una de varias técnicas para la reducción de dimensionalidad en el aprendizaje automático, se basa en gran medida en el rango de la matriz de covarianza al seleccionar características para ser reducidas basado en el rango; PCA puede identificar características significativas basadas en el rango para ayudar a reducir eficientemente las dimensiones mientras aún se preserva la información esencial. PCA permite a los profesionales encontrar rápidamente características significativas de su conjunto de datos mientras mantienen detalles esenciales. El reconocimiento de imágenes utiliza extensamente PCA ya que reduce la complejidad computacional, además de ayudar a prevenir el sobreajuste simplificando los datos de la imagen con una matriz de menor rango que captura su estructura principal, haciendo modelos más rápidos y manteniendo la precisión intacta.
Compresión de Imágenes
Los métodos de compresión de imágenes como JPEG dependen de aproximaciones de matrices de bajo rango para reducir eficientemente el tamaño de los archivos mientras mantienen la calidad visual. Al aplicar la Descomposición en Valores Singulares (SVD) a una matriz de imágenes, solo se conservan sus componentes más significativos (valores singulares), mientras que se pierde menos datos esenciales como "valores no importantes". Como resultado de aplicar esta aproximación de bajo rango para crear archivos comprimidos que casi lucen exactamente igual pero ocupan significativamente menos espacio de almacenamiento; haciendo que JPEG sea ideal para fotografías digitales y videos cotidianos.
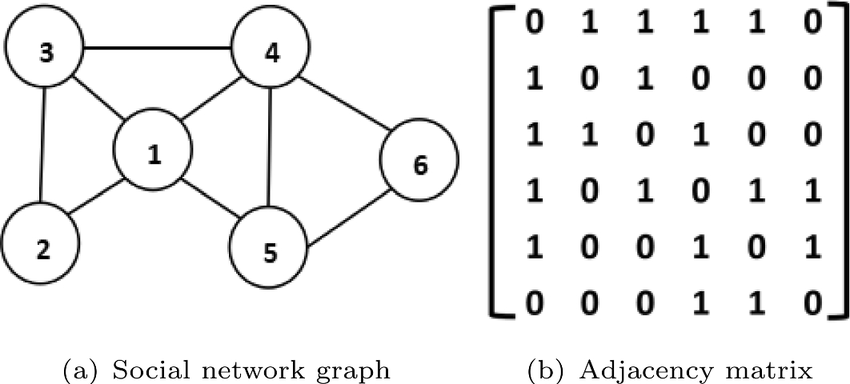
Análisis de Redes
Los rangos de las matrices de adyacencia proporcionan información vital sobre la estructura y conectividad de redes como las de medios sociales. Revelan comunidades independientes o conexiones redundantes dentro de un círculo social superpuesto; las matrices de adyacencia de bajo rango pueden revelar grupos agrupados mientras que las de rango completo indican redes más distribuidas e interconectadas; tal análisis ayuda a identificar nodos clave u optimizar diseños de red en áreas como sistemas de comunicación o redes de transporte.
Sensibilidad del Rango
Pequeñas perturbaciones en los datos (por ejemplo, ruido) pueden cambiar el rango de una matriz al introducir o eliminar la independencia lineal. Comprender esta sensibilidad mejora los métodos para manejar conjuntos de datos ruidosos en disciplinas como la biología computacional o el procesamiento de señales.
Preguntas Frecuentes sobre Cómo Encontrar el Rango de una Matriz
Preguntas Populares
¿Puede el rango de una matriz exceder su dimensión más pequeña?
No, el rango de una matriz no puede exceder su dimensión más pequeña. Para cualquier matriz \(A\) de tamaño \(m \times n\), su rango satisface \(\text{rank}(A) \leq \min(m, n)\). Esta limitación surge de la definición de rango, ya que representa el número máximo de filas o columnas linealmente independientes en la matriz. En un sentido geométrico, el rango refleja la dimensionalidad del espacio abarcado por las filas o columnas de la matriz, y esto no puede exceder el número real de filas (\(m\)) o columnas (\(n\)) disponibles.
Por ejemplo, considere una \(2 \times 3\) matriz. Aunque tiene tres columnas, puede abarcar como máximo un subespacio de 2 dimensiones en un espacio de 3 dimensiones porque hay solo dos filas para proporcionar vectores únicos. Este principio asegura que el rango de la matriz respete las restricciones de sus dimensiones físicas.
¿Por qué siempre son iguales los rangos de fila y columna?
La igualdad del rango de filas y el rango de columnas es un resultado indispensable en álgebra lineal, fundamentado en su relación con las transformaciones de matrices, específicamente la igualdad entre las dimensiones del espacio de filas y las dimensiones del espacio de columnas bajo cualquier transformación de matriz. Las operaciones elementales de fila aseguran esto manteniendo la independencia lineal tanto para filas como para columnas; esta propiedad reside en su núcleo gracias a que cualquier matriz \(A\) puede transformarse en su forma escalonada de filas mientras aún mantiene su rango; cada fila no nula (rango de fila) corresponde directamente con el conteo de columnas independientes (rango de columna).
Por ejemplo, si una matriz tiene tres filas linealmente independientes, el espacio de columnas correspondiente también debe abarcar tres dimensiones. Este resultado garantiza que las dimensiones de los dos espacios vectoriales—filas y columnas—estén intrínsecamente vinculadas, conduciendo a la propiedad clave: \(\text{row rank} = \text{column rank} = \text{rank}(A)\).
¿Por qué son comunes en la práctica las matrices deficientes en rango?
Los sistemas del mundo real a menudo incluyen matrices deficientes en rango debido a la redundancia de datos, ruido de medición o valores faltantes que reducen el contenido de información de la matriz; la deficiencia de rango ocurre cuando algunas filas o columnas dependen linealmente unas de otras, reduciendo el contenido de información efectivo de la matriz - esto suele ocurrir con conjuntos de datos con variables relacionadas y medidas repetidas que superponen información y llevan a filas/columnas redundantes en una estructura de matriz por lo demás efectiva.
Considere, por ejemplo, una matriz de datos donde se registran tanto la edad como el año de nacimiento; dado que estas variables están matemáticamente entrelazadas, su inclusión crea redundancia, resultando en una deficiencia de rango en su forma matricial. Las redes de sensores con múltiples sensores midiendo fenómenos similares a menudo experimentan este problema, con lecturas superpuestas que disminuyen su valor de rango con el tiempo.
La deficiencia de rango puede volverse aún más prevalente cuando se trabaja con conjuntos de datos ruidosos o incompletos, debido a los errores de medición que introducen inconsistencias o datos faltantes que agotan la independencia lineal a través de filas o columnas. Sin embargo, entender y analizar matrices deficientes en rango sigue siendo vital al aplicar técnicas de aprendizaje automático, procesamiento de señales o estadísticas en conjuntos de datos ruidosos o incompletos.
Conclusión
Comprender el rango de una matriz conecta conceptos teóricos con aplicaciones prácticas en la vida cotidiana. Desde el uso de técnicas tradicionales de REF o enfoques más modernos como la descomposición en valores singulares (SVD) para comprender mejor sus diversas propiedades – como encontrar soluciones de sistemas lineales hasta aplicaciones en la compresión de imágenes – entender el rango de una matriz simplifica tanto las aplicaciones teóricas como prácticas del álgebra lineal.
El dominio del rango de una matriz puede proporcionarte las herramientas necesarias para abordar problemas en disciplinas de matemáticas, ciencias e ingeniería, proporcionando soluciones computacionales precisas y entendimiento sobre las estructuras de datos. Así que adelante, ¡calcula ese rango! Te dará acceso a entender cómo operan los cálculos de matrices.
Referencia:
https://www.cs.cmu.edu/~venkatg/teaching/CStheory-infoage/book-chapter-4.pdf
Artículos relacionados
Sophia Greene
Dec 24, 2024
Alice Brooks
Dec 23, 2024
Alice Brooks
Feb 13, 2025
Alice Brooks
Feb 13, 2025
Isaac Turner
Dec 25, 2024
Alice Brooks
Dec 17, 2024
Alice Brooks
Feb 14, 2025
Sophia Greene
Dec 24, 2024
Alice Brooks
Dec 23, 2024
Alice Brooks
Feb 13, 2025
Alice Brooks
Feb 13, 2025
Isaac Turner
Dec 25, 2024
Alice Brooks
Dec 17, 2024
