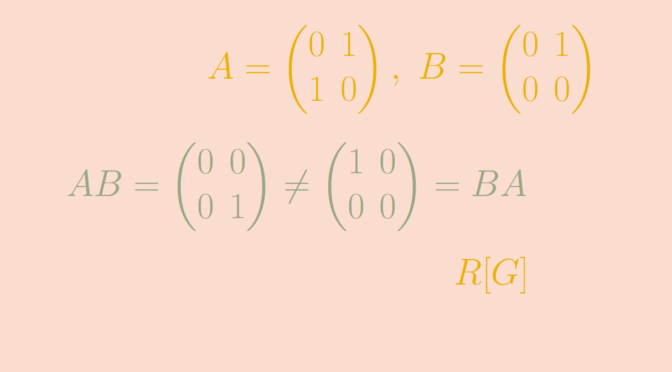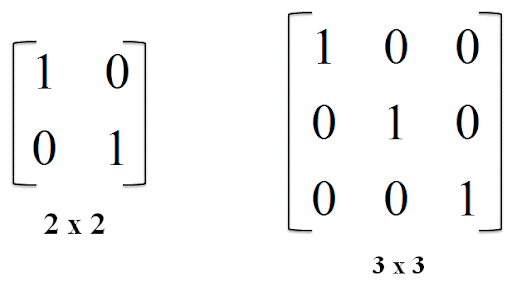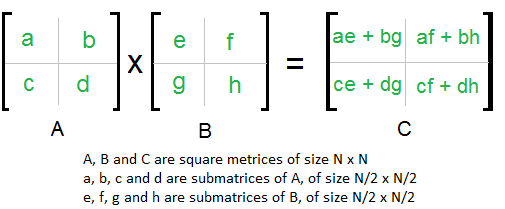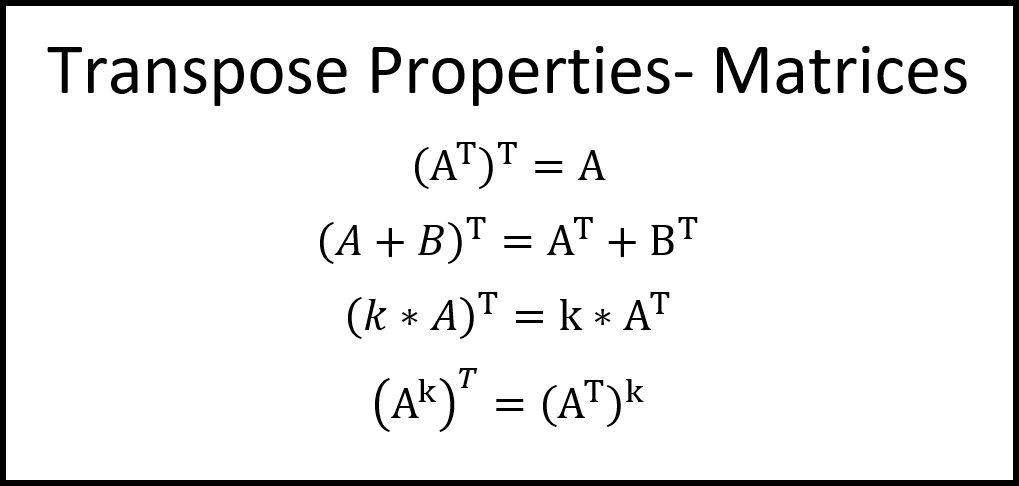Cómo Multiplicar Matrices: Una Guía Completa

¿Qué es la Multiplicación de Matrices?

Definición de Multiplicación de Matrices

Una matriz es una colección estructurada y bidimensional de números, símbolos o expresiones matemáticas organizadas sistemáticamente en filas y columnas, formando una estructura rectangular en forma de cuadrícula. Las matrices sirven como constructos fundamentales de las matemáticas en álgebra lineal, así como en muchas de sus ramas, con aplicaciones en campos más allá de las matemáticas, como la ciencia y la ingeniería. Muchos científicos consideran las matrices como soluciones ideales de almacenamiento y medios efectivos para realizar operaciones sofisticadas, siendo la multiplicación de matrices una de esas operaciones que las hace muy convenientes.

La multiplicación de matrices es una operación elemental utilizada en álgebra lineal que combina dos matrices y produce otra matriz conocida como la matriz producto, comúnmente utilizada para representar transformaciones lineales, resolver sistemas de ecuaciones y modelar fenómenos del mundo real matemáticamente.

Una característica esencial de la multiplicación de matrices es que sigue una estricta regla de compatibilidad: las columnas de la primera matriz deben corresponder en número a las filas de la segunda matriz. En términos más simples, dos matrices solo pueden multiplicarse si las "dimensiones internas" coinciden.

Ejemplo: Si una matriz tiene dimensiones m×n (m filas por n columnas) mientras que otra tiene dimensiones n×p, la multiplicación debería ser válida y producir una matriz de salida con dimensiones de m×p; de lo contrario, se volvería indefinida y la operación desconocida.

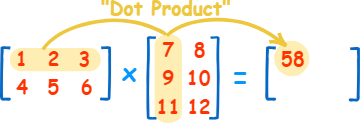
Esta regla se deriva de cómo se combinan los elementos de las matrices: cada entrada en la matriz producto representa un resultado del producto punto entre las filas de una matriz y las columnas de otra matriz, por lo que la alineación de dimensiones se convierte en crítica para operaciones exitosas de multiplicación de matrices en diferentes disciplinas. La multiplicación de matrices no solo captura relaciones numéricas, sino también conexiones geométricas o algebraicas, consolidándose como una herramienta esencial de operación matemática.

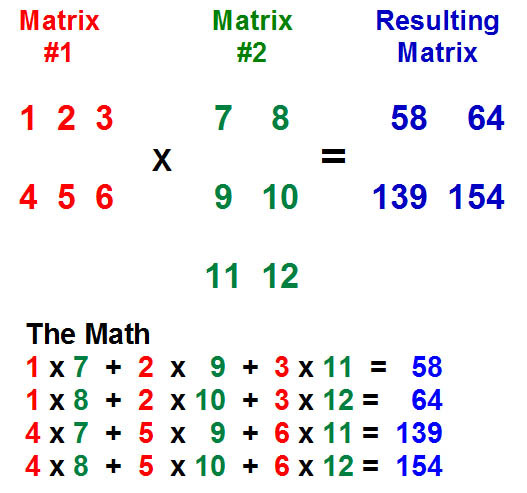
Por ejemplo:

La Matriz A es 2×3 :

\(\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 &6\end{bmatrix}\)

La Matriz B es 3×2 :

\(\begin{bmatrix} 7 &8 \\ 9 & 10\\ 11 &12\end{bmatrix}\)

El producto de A y B será una matriz 2×2.

Aplicaciones e Importancia

La multiplicación de matrices ha sido considerada durante mucho tiempo una técnica indispensable en informática, física y economía por su capacidad para tratar eficazmente con relaciones de datos complejas. Las técnicas de Inteligencia Artificial/ML también dependen en gran medida de la multiplicación de matrices, por ejemplo, al entrenar redes neuronales, reconocimiento de imágenes, procesamiento de texto o modelado predictivo. Las tecnologías modernas de hoy en día a menudo emplean operaciones de matrices directamente. Tareas como el reconocimiento facial o sistemas de recomendación también dependen en gran medida de las operaciones con matrices; su presencia es, por tanto, integral.

La multiplicación de matrices es esencial en varios campos, como la mecánica cuántica y la economía, donde modela estados y transformaciones cuánticos o ayuda en el análisis de optimización de oferta, demanda y recursos. Además, su versatilidad sirve como la base del avance en numerosos campos científicos y técnicos por igual.

Antecedentes Históricos e Ideas

Orígenes de la Multiplicación de Matrices

La multiplicación de matrices se remonta al trabajo pionero de Jacques Philippe Marie Binet de Francia sobre transformaciones lineales y sistemas de ecuaciones lineales en 1812. Binet fue pionero en la multiplicación de matrices como una herramienta analítica. Sus contribuciones fueron motivadas principalmente por la necesidad de desarrollar formas eficientes de representar y resolver sistemas, los cuales eran componentes centrales de las matemáticas y ciencias aplicadas del siglo XIX. Binet inicialmente se enfocó en su trabajo en ecuaciones lineales; su enfoque revolucionario finalmente sentó las bases para el álgebra lineal como un campo. Con el tiempo, la multiplicación de matrices se convirtió en uno de sus distintivos, proporcionando conocimientos más profundos sobre los espacios vectoriales y las transformaciones, impactando muchas áreas diferentes de las matemáticas y la ciencia.

Papel Actual en la Matemática

La multiplicación de matrices ha crecido rápidamente más allá de sus raíces para convertirse en una de las herramientas más versátiles y potentes disponibles para las matemáticas modernas. Ahora se utiliza en diversas disciplinas, desde ciencias puras hasta aplicadas. Las matrices son críticas en la mecánica cuántica, representando operadores que calculan probabilidades y describen los comportamientos de los sistemas cuánticos. Las matrices ayudan a modelar fenómenos complejos que de otro modo serían difíciles de formalizar usando medios más tradicionales. La criptografía utiliza principios y códigos matemáticos para cifrar y transformar datos de manera segura, proporcionando una base matemática para proteger nuestra información digitalmente almacenada en esta era digital. Las matrices ofrecen un medio eficiente de resolver problemas de optimización que se encuentran en la ingeniería, la informática y la economía al simplificar los cálculos para encontrar soluciones eficientes a sistemas altamente complejos. Impulsando los avances en inteligencia artificial y aprendizaje automático, las multiplicaciones de matrices a gran escala juegan un papel esencial en el entrenamiento de redes neuronales, sintiéndose sus efectos en campos tan diversos como el reconocimiento de imágenes, el procesamiento del lenguaje natural y los sistemas autónomos.

La multiplicación de matrices tiene muchas aplicaciones y se erige como un componente indispensable, no solo en las matemáticas teóricas sino también para resolver problemas prácticos en un espectro de campos científicos y tecnológicos.

Reglas y Condiciones para la Multiplicación de Matrices

Reglas Fundamentales de la Multiplicación de Matrices

Regla de Compatibilidad

Para que ocurra la multiplicación de matrices, las dimensiones de las dos matrices deben adherirse a lo siguiente:

Si la Matriz A tiene dimensiones m×n y la Matriz B tiene dimensiones n×p, son compatibles.

La matriz resultante, Matriz C, tendrá dimensiones m×p.

Por ejemplo:

Matriz A (2×3):

\(\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 &6\end{bmatrix}\)

Matriz B (3×2):

\(\begin{bmatrix} 7 &8 \\ 9 & 10\\ 11 &12\end{bmatrix}\)

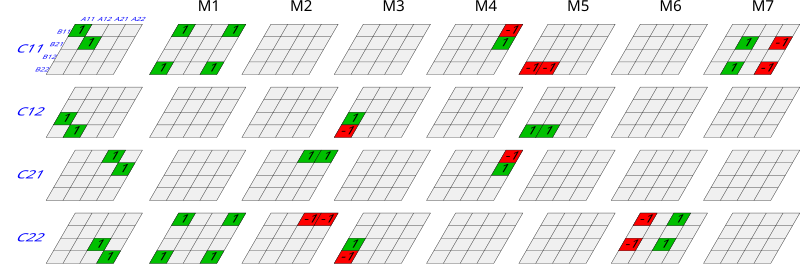
Matriz C (2×2) se calcula así:

\(\begin{bmatrix} C11 & C12\\ C21 &C22\end{bmatrix}\)

Ejemplos de Compatibilidad

Una matriz 3×2 puede multiplicarse por una matriz 2×4, dando como resultado una matriz 3×4.

Una matriz 4×3 no puede ser multiplicada por otra matriz 4×3 porque las dimensiones no cumplen con el requisito de compatibilidad.

Conmutatividad y Casos Especiales

No Conmutatividad de la Multiplicación de Matrices

La multiplicación de matrices, a diferencia de la multiplicación escalar, no es conmutativa. Generalmente, AB ≠ BA, incluso si ambos productos están definidos.

Por ejemplo:

Sean A y B dos matrices 2×2:

\(A=\begin{bmatrix}1 &2\\ 3 &4\end{bmatrix}\)

\(B=\begin{bmatrix}5 &6\\ 7 &8\end{bmatrix}\)

Matriz AB:

\(\begin{bmatrix}1*5+2*7 &1*6+2*8\\ 3*5+4*7 &3*6+4*8\end{bmatrix}\)

\(=\begin{bmatrix}19 &22\\ 43 &50\end{bmatrix}\)

Matriz BA:

\(\begin{bmatrix}5*1+6*3 &5*2+6*4\\ 7*1+8*3 &7*2+8*4\end{bmatrix} =\begin{bmatrix}23 &34\\ 31 &46\end{bmatrix}\)

Claramente, AB ≠ BA.

Importancia del Orden en Aplicaciones del Mundo Real

Esta propiedad tiene implicaciones en la vida real. Por ejemplo, en logística, el orden de la multiplicación de matrices determina cómo fluye la información de la cadena de suministro a través de ubicaciones geográficas, afectando estrategias operativas y eficiencia.

Matrices Identidad y Cero

Matriz Identidad

Una matriz identidad, denotada por I, es una matriz cuadrada con 1’s en su diagonal principal y 0’s en otras posiciones. Preserva los valores de otras matrices durante la multiplicación. Para cualquier matriz A:

A × I = A o I × A = A

Por ejemplo:

Matriz Identidad (3×3):

\(\begin{bmatrix} 1&0 & 0\\ 0 &1 &0 \\0 & 0 &1\end{bmatrix}\)

Matriz Cero

Una matriz cero, denotada como O, consiste únicamente de 0’s. Cualquier matriz multiplicada por la matriz cero da otra matriz cero:

A × O = O

Más Allá de las Matemáticas

Estas matrices especiales destacan la presencia de dependencias o restricciones dentro de los sistemas, reforzando los principios de dependencia en campos como la física o los modelos de datos.

Multiplicación de Matrices Paso a Paso

Entendiendo las Operaciones de Producto Punto

Fórmula del Multiplicador Fila-por-Columna

Calcular cada elemento de la matriz producto implica realizar el producto punto entre una fila de la primera matriz y una columna de la segunda:

Matriz A:

\(\begin{bmatrix} 1& 2\\ 3&4\end{bmatrix}\)

Matriz B:

\(\begin{bmatrix} 5& 6\\ 7&8\end{bmatrix}\)

Calcular C[1,1]: (1×5) + (2×7) = 5 + 14 = 19

Calcular C[1,2]: (1×6) + (2×8) = 6 + 16 = 22

Calcular C[2,1]: (3×5) + (4×7) = 15 + 28 = 43

Calcular C[2,2]: (3×6) + (4×8) = 18 + 32 = 50

Matriz Resultante C:

\(\begin{bmatrix} 19& 22\\ 43&50\end{bmatrix}\)

Errores Comunes

Al realizar este cálculo manualmente, los errores más comunes involucran:

Desalinear filas y columnas

Olvidar asegurar que las dimensiones de las matrices sean compatibles

Técnicas de Cálculo Manual

Ayudas Visuales y Herramientas

Para simplificar cálculos manuales:

Usa cuadrículas para alinear los elementos fila-por-columna.

Resalta o encierra en un círculo los valores correspondientes que están siendo multiplicados.

Trucos para Enfrentar Matrices Grandes

Para matrices más grandes como 4×4 o 5×5:

Divide la matriz en bloques más pequeños.

Enfócate en calcular un cuadrante o submatriz a la vez.

Multiplicación de Matrices con Diferentes Dimensiones

La multiplicación de matrices puede tomar muchas formas dependiendo de las dimensiones de las matrices involucradas. Aunque las matrices pequeñas (por ejemplo, 2×2) son más fáciles de calcular manualmente, las matrices más grandes (como las 3×3 o de dimensiones altas) a menudo requieren técnicas computacionales. Esta sección explora el proceso paso a paso para manejar matrices de diferentes dimensiones y demuestra ejemplos prácticos.

Multiplicación de Matrices 2×2

Calcular el producto de dos matrices 2×2 es un proceso sencillo. Dadas dos matrices, A y B:

A =

\(\begin{bmatrix} a& b\\ c&d\end{bmatrix}\)

B =

\(\begin{bmatrix} e& f\\ g&h\end{bmatrix}\)

La matriz producto C = AB también tendrá dimensiones 2×2, y sus elementos se calculan como:

C =

\(\begin{bmatrix} ae+bg& af+bh\\ ce+dg&cf+dh\end{bmatrix}\)

Ejemplo

Supongamos:

A = \(\begin{bmatrix} 1& 2\\ 3&4\end{bmatrix}\)

B = \(\begin{bmatrix} 5& 6\\ 7&8\end{bmatrix}\)

La matriz resultante C se calcula como:

C[1,1] = (1*5) + (2*7) = 5 + 14 = 19  

C[1,2] = (1*6) + (2*8) = 6 + 16 = 22  

C[2,1] = (3*5) + (4*7) = 15 + 28 = 43  

C[2,2] = (3*6) + (4*8) = 18 + 32 = 50

Así,

C = \(\begin{bmatrix} 19& 22\\ 43&50\end{bmatrix}\)

Aplicaciones de las Matrices 2×2

Las matrices 2×2 se utilizan ampliamente en física para dinámicas de sistemas simples, como sistemas masa-resorte o transformaciones 2D (por ejemplo, escalado, rotación).

H3: Multiplicación de Matrices 3×3

Para matrices 3×3, los principios son los mismos, pero los cálculos aumentan en complejidad debido al mayor número de elementos. Las matrices A y B, ambas de dimensiones 3×3, se definen como:

A = \(\begin{bmatrix} a & b &c \\ d & e &f \\ g & h &i\end{bmatrix}\)

B = \(\begin{bmatrix} j & k &l \\ m& n & o \\ p & q & r\end{bmatrix}\)

La matriz resultante C = AB se calcula tomando el producto punto de cada fila de A con cada columna de B. Cada elemento de C[i, j] se calcula como:

C[i, j] = A[i,1] × B[1,j] + A[i,2] × B[2,j] + A[i,3] × B[3,j]

Ejemplo

Dado:

A = \(\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{bmatrix}\)

B = \(\begin{bmatrix} 10 & 11 & 12 \\ 13 & 14 & 15 \\ 16 & 17 & 18\end{bmatrix}\)

Calculando el primer elemento C[1,1] :

C[1,1] = (1*10) + (2*13) + (3*16) = 10 + 26 + 48 = 84

De manera similar, calcula el resto para obtener:

\(\begin{bmatrix} 84 & 90 & 96 \\ 201 & 216 & 231 \\ 318 & 342 & 366\end{bmatrix}\)

Aplicaciones de las Matrices 3×3

Las matrices 3×3 se utilizan frecuentemente en ingeniería (por ejemplo, matrices de rigidez en el análisis de cerchas).

En gráficos por computadora en 3D, representan transformaciones como rotaciones y escalado en el espacio.

Multiplicación de Matrices de Alta Dimensión

La multiplicación se vuelve computacionalmente costosa para matrices de dimensiones mayores como 4x4, 100x100, o más; el número de operaciones aumenta asintóticamente con la dimensión; las operaciones típicas requieren O(n³) operaciones si se realizan de manera ingenua; por lo tanto, la mayoría de las matrices de alta dimensión deben manejarse utilizando algoritmos avanzados o software como la biblioteca NumPy de Python, MATLAB o TensorFlow diseñados para propósitos de aprendizaje automático.

Desafíos de las Matrices de Alta Dimensión

Uso de Memoria: Las matrices grandes requieren una cantidad considerable de memoria, especialmente cuando se implementan en hardware como GPUs.

Tiempo Computacional: Más dimensiones incrementan exponencialmente el tiempo computacional a menos que se usen algoritmos optimizados como el algoritmo de Strassen.

Ejemplo de Multiplicación a Gran Escala Simplificada

Sea A una matriz 100×50 y B una matriz 50×100. Ya que cada una de las 100 filas en A debe ser multiplicada por todas las columnas de B, se requieren un total de 100×100 = 10,000 productos punto.

Conclusiones Clave

Comienza con matrices de dimensiones más pequeñas para desarrollar intuición sobre las reglas de multiplicación.

Las herramientas software son esenciales para manejar operaciones a gran escala en aplicaciones del mundo real como el aprendizaje automático o la mecánica cuántica.

Propiedades de la Multiplicación de Matrices

La multiplicación de matrices tiene varias propiedades matemáticas importantes que dictan cómo se comporta en diferentes escenarios. Estas incluyen las propiedades asociativa, distributiva y de transposición. Además, los determinantes y casos especiales como matrices diagonales e identidad conducen a resultados únicos en la multiplicación.

Asociatividad de la Multiplicación de Matrices

La multiplicación de matrices satisface la propiedad asociativa. Para las matrices A, B y C, siempre que sean compatibles para la multiplicación:

(AB)C = A(BC)

Ejemplo

Sea:

A = \(\begin{bmatrix} 1 & 2\\ 3 & 4\end{bmatrix}\)

B = \(\begin{bmatrix} 5 & 6\\ 7 & 8\end{bmatrix}\)

C =\(\begin{bmatrix} 9 & 10\\ 11 & 12\end{bmatrix}\)

Primero, calcula (AB)C : \(\begin{bmatrix} 19 & 22\\ 43 & 50\end{bmatrix}\)

Luego, multiplica por C:

[(AB)C] =  \(\begin{bmatrix} 19*9 + 22*11 & 19*10 + 22*12\\ 43*9 + 50*11 & 43*10 + 50*12\end{bmatrix}\)

Resultando en: \(\begin{bmatrix} 437 & 494\\ 1013 & 1146\end{bmatrix}\)

Ahora, calcula A(BC) :

BC =  \(\begin{bmatrix} 152 & 168\\ 208 & 230\end{bmatrix}\)

Luego, multiplica A por este resultado:

A(BC) =\(\begin{bmatrix} 437 & 494\\ 1013 & 1146\end{bmatrix}\)

El resultado final confirma la asociatividad.

Distributividad de la Multiplicación de Matrices

La multiplicación de matrices también satisface la propiedad distributiva:

A(B + C) = AB + AC

Ejemplo

Sea:

A = [1 2]  

B = [3 4]  

C = [5 6]

Calcula AB + AC y compáralo con A(B+C). Ambos enfoques producen el mismo resultado.

Propiedad de Transposición

Para las matrices A y B :

(AB)^T = B^T A^T

Esta propiedad es crítica en geometría y visión por computadora para rotar o escalar datos.

Aplicaciones Reales de la Multiplicación de Matrices

La multiplicación de matrices juega un papel vital en diversos dominios, impulsando innovaciones y resolviendo problemas complejos en campos como el aprendizaje automático, los gráficos por computadora y la física. Lejos de ser una abstracción matemática, es fundamental para numerosas aplicaciones y tecnologías del mundo real.

Aprendizaje Automático e Inteligencia Artificial

La multiplicación de matrices está en el núcleo de los sistemas de aprendizaje automático e inteligencia artificial, ayudando a que los sistemas aprendan, predigan y reconozcan patrones. Una función clave de la multiplicación de matrices se encuentra dentro de las redes neuronales, un elemento indispensable en muchos programas de inteligencia artificial que abarcan desde el reconocimiento de imágenes hasta el procesamiento del lenguaje natural.

Las redes neuronales se basan en matrices de pesos que definen las relaciones entre las neuronas. Cuando una matriz de entrada (por ejemplo, valores de píxeles o incrustaciones de texto) pasa a través de cada capa, se multiplica con matrices de pesos para crear salidas transformadas que contienen características extraídas, como bordes en imágenes o significado semántico en oraciones para tareas como clasificación, traducción o reconocimiento de imágenes.

Los modelos de aprendizaje profundo implican millones de operaciones de multiplicación de matrices durante el entrenamiento. Estos cálculos permiten que la red ajuste y refine sus pesos mediante técnicas como la retropropagación para obtener la máxima precisión y funcionalidad. La multiplicación de matrices también constituye una base esencial para los sistemas de recomendación; técnicas como el filtrado colaborativo o la factorización de matrices se utilizan para predecir preferencias de usuarios mediante estos métodos; plataformas como Amazon o Netflix dependen en gran medida de tales capacidades de predicción para ofrecer experiencias personalizadas a miles de millones de clientes en todo el mundo.

Las GPUs y TPUs, específicamente diseñadas para cálculos de matrices a gran escala, han revolucionado las aplicaciones de inteligencia artificial, como vehículos autónomos, asistentes virtuales, y detección de fraudes en tiempo real, haciendo que la inteligencia artificial sea mucho más accesible y eficiente.

Gráficos por Computadora

La multiplicación de matrices está en el núcleo de los gráficos por computadora, permitiendo la manipulación y renderización de objetos en espacios 2D y 3D. La multiplicación de matrices también respalda transformaciones esenciales como escalado, rotación y traducción que permiten a los artistas digitales producir visuales realistas en películas animadas, videojuegos y simulaciones.

Imagina jugar un videojuego: cada objeto en su mundo está representado como una matriz de coordenadas, por lo que cuando los personajes se mueven o la cámara cambia, la multiplicación de matrices recalcula estas coordenadas para reflejar sus nuevas posiciones, asegurando una animación fluida. Una matriz de rotación puede alterar la orientación de un objeto mientras que una matriz de traducción desplaza su ubicación dentro de escenas; al encadenar múltiples transformaciones juntas mediante sucesivas multiplicaciones de matrices, los objetos pueden moverse y cambiar de tamaño dinámicamente según sea necesario.

La multiplicación de matrices juega un papel integral en entornos 3D, particularmente en procesos como la proyección en perspectiva. La proyección en perspectiva consiste en mapear objetos 3D en una pantalla 2D para simular profundidad y realismo, utilizada ampliamente por sistemas de realidad virtual (VR) y realidad aumentada (AR) para ajustar escenas de acuerdo con los movimientos del usuario. Los ajustes en tiempo real impulsados por la multiplicación de matrices permiten a los usuarios interactuar naturalmente dentro de un mundo creado artificialmente.

El software de diseño asistido por computadora (CAD) aprovecha la multiplicación de matrices para permitir a arquitectos y diseñadores manipular geometrías de objetos con mayor precisión; sin esta base matemática, no serían posibles sistemas inmersivos, simulaciones realistas y visuales cinematográficos en juegos o películas.

Física e Ingeniería

La física y la ingeniería utilizan extensamente la multiplicación de matrices para modelar sistemas, resolver ecuaciones y optimizar diseños. Muchos fenómenos físicos, desde la mecánica clásica hasta la mecánica cuántica, se expresan matemáticamente a través de matrices.

En ingeniería estructural, el análisis de elementos finitos (FEA) implica dividir una estructura en pequeños componentes (elementos finitos) y representar su comportamiento—tensión, deformación y desplazamiento—usando matrices. Al multiplicar y combinar estas matrices, los ingenieros pueden predecir cómo responderán edificios, puentes o vehículos a fuerzas como cargas o vibraciones. Este proceso asegura la seguridad y eficiencia de diseños que van desde rascacielos hasta aeronaves.

Las operaciones con matrices se han utilizado durante mucho tiempo en física para resolver sistemas acoplados de ecuaciones que se refieren a la mecánica orbital o interacciones de partículas. La mecánica cuántica particularmente depende de esta base matemática para representar estados y operadores usando vectores y matrices; transformaciones de funciones de onda son un ejemplo modelado mediante la multiplicación entre estas matrices, mientras que la computación cuántica también utiliza técnicas de multiplicación de matrices para describir puertas cuánticas o simular manipulaciones de cúbits.

La multiplicación de matrices también facilita el análisis de circuitos eléctricos donde componentes como resistencias o voltajes forman redes interconectadas, utilizando las leyes de circuitos de Kirchhoff expresadas como multiplicación de matrices para llegar a soluciones sistemáticas a sistemas eléctricos complejos. Los sistemas de robótica y control también utilizan la multiplicación de matrices como un método efectivo para identificar trayectorias de movimiento precisas para brazos robóticos o vehículos autónomos.

La multiplicación de matrices desempeña un papel esencial al conectar la teoría matemática con aplicaciones prácticas en ingeniería y ciencias, desde simular dinámicas físicas hasta optimizar diseños estructurales o procesar sistemas energéticos.

La multiplicación de matrices ha emergido como un componente indispensable en la configuración de avances en aprendizaje automático, gráficos por computadora y física. Desde impulsar sistemas de inteligencia artificial hasta renderizar visuales realistas y resolver desafíos científicos, las aplicaciones de la multiplicación de matrices demuestran su profundo efecto en la configuración de tecnologías mientras resuelven problemas del mundo real.

Desafíos en la Multiplicación de Matrices

La multiplicación de matrices, una operación fundamental en matemáticas computacionales, enfrenta varios desafíos debido a su complejidad computacional y numérica inherente.

Errores Numéricos

La multiplicación de matrices depende en gran medida de la aritmética de punto flotante, que es inherentemente propensa a errores de redondeo debido a la precisión finita de las representaciones informáticas. Al multiplicar matrices grandes o manejar datos de alta dimensión, estos pequeños errores pueden acumularse, lo que potencialmente conduce a inexactitudes significativas en el resultado final. Este problema se vuelve más pronunciado en procesos iterativos o aplicaciones como el aprendizaje automático y las simulaciones científicas, donde las matrices se multiplican repetidamente.

Complejidad Computacional

El método de fuerza bruta para la multiplicación de matrices tiene una complejidad de tiempo de O(n³); es decir, su tiempo de ejecución aumenta cúbicamente a medida que el tamaño de la matriz crece. A medida que los conjuntos de datos se expanden en campos como la inteligencia artificial, el análisis de grandes datos y la computación científica, esto se vuelve computacionalmente costoso y lleva mucho tiempo, potencialmente convirtiéndose en prohibitivo en términos de tiempo y costo al tratar con operaciones en matrices muy grandes.

Soluciones Optimizadas

Algoritmo de Strassen

El algoritmo de Strassen optimiza la multiplicación de matrices tradicional al reducir el número de multiplicaciones involucradas. Aunque no elimina completamente el crecimiento cúbico, reduce la complejidad a aproximadamente O(n².81), haciéndolo más rápido para matrices suficientemente grandes. Sin embargo, el algoritmo introduce una sobrecarga adicional, como la partición compleja de datos y un mayor uso de memoria, lo que puede afectar su rendimiento en el mundo real.

Procesamiento Paralelo

El procesamiento paralelo utiliza CPUs multicore o GPUs para distribuir la multiplicación de matrices entre varios procesadores o núcleos y acelerarla, acelerando significativamente el cálculo. Marcos a gran escala como CUDA para GPUs o sistemas de computación distribuida como Apache Spark pueden utilizarse para acelerar estas operaciones significativamente, aunque este enfoque reduce considerablemente los tiempos de cómputo mientras crea desafíos relacionados con la sincronización de datos y la sobrecarga de comunicación entre procesadores.

Conclusión y Perspectivas Futuras

La multiplicación de matrices es más que una operación matemática: sirve como una poderosa herramienta que modela, calcula y resuelve problemas multidimensionales y multivariados que nos rodean cada día. Desde diseñar sistemas de transporte hasta enseñar a la inteligencia artificial a predecir resultados con precisión, multiplicar matrices correctamente nos permite considerar sistemáticamente todos los elementos dentro de los complejos sistemas que conforman la vida a nuestro alrededor.

A través de este artículo, hemos explorado cómo funciona la multiplicación de matrices y cuándo y cómo debería emplearse a través de las disciplinas. En particular, identificamos reglas sobre la compatibilidad de dimensiones, asociatividad, así como desafíos como la eficiencia computacional y los errores de precisión que surgen con esta metodología.

El pensamiento innovador solo aumentará su significado; la multiplicación de matrices sirve como la piedra angular de campos de vanguardia como la computación cuántica, donde las transformaciones de estados cuánticos dependen de la multiplicación de matrices; la IA utiliza pesos codificados dentro de redes neuronales para impulsar chatbots y servicios de reconocimiento de imágenes, entre muchas otras cosas;

La multiplicación de matrices tiene un gran potencial en campos novedosos como la medicina personalizada y la simulación ambiental, donde conjuntos de datos grandes requieren cálculos robustos pero escalables para analizarlos de manera efectiva. Dominar esta operación matemática no solo facilita las carreras dentro de las disciplinas STEM, sino que puede ser la solución a algunos de los problemas más difíciles de hoy en día.

La multiplicación de matrices sirve como tu guía para navegar relaciones interdependientes, ya sean rutas de metro, algoritmos de IA, sistemas dinámicos en física o la escala de sistemas dinámicos. A medida que continuamos explorando la innovación dentro del cálculo y las aplicaciones, esta poderosa operación permanecerá en el núcleo del progreso.

Referencia:

https://medium.com/analytics-vidhya/linear-algebra-how-uses-in-artificial-intelligence-2e1e001c65

https://www.reddit.com/r/QuantumComputing/comments/1e0x1ad/can_quantum_computers_do_matrix_multiplications/

https://mathoverflow.net/questions/101531/how-fast-can-we-really-multiply-matrices