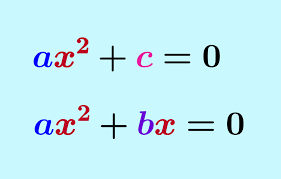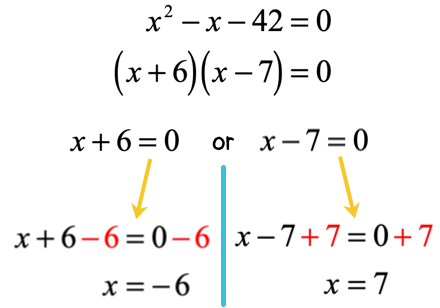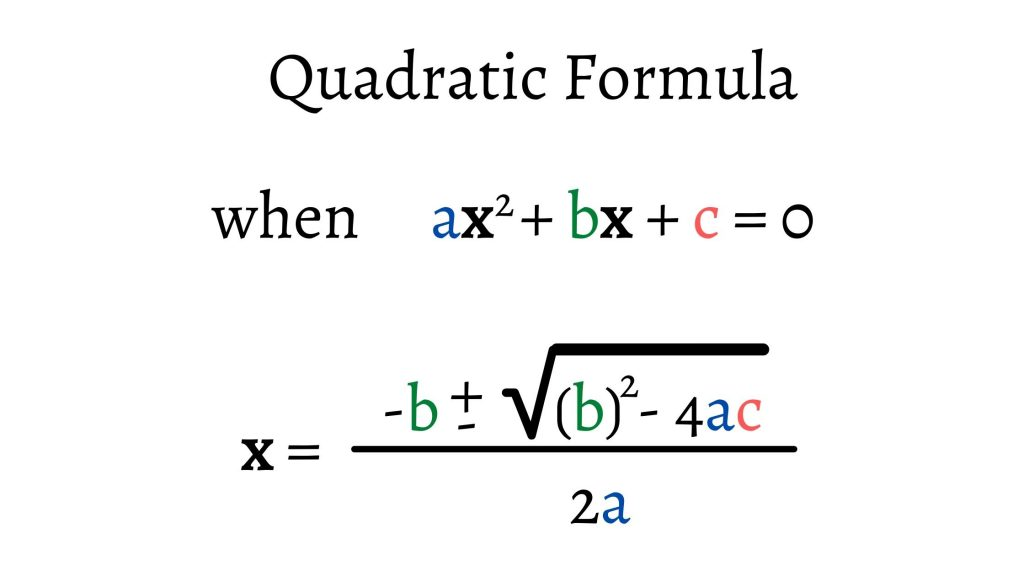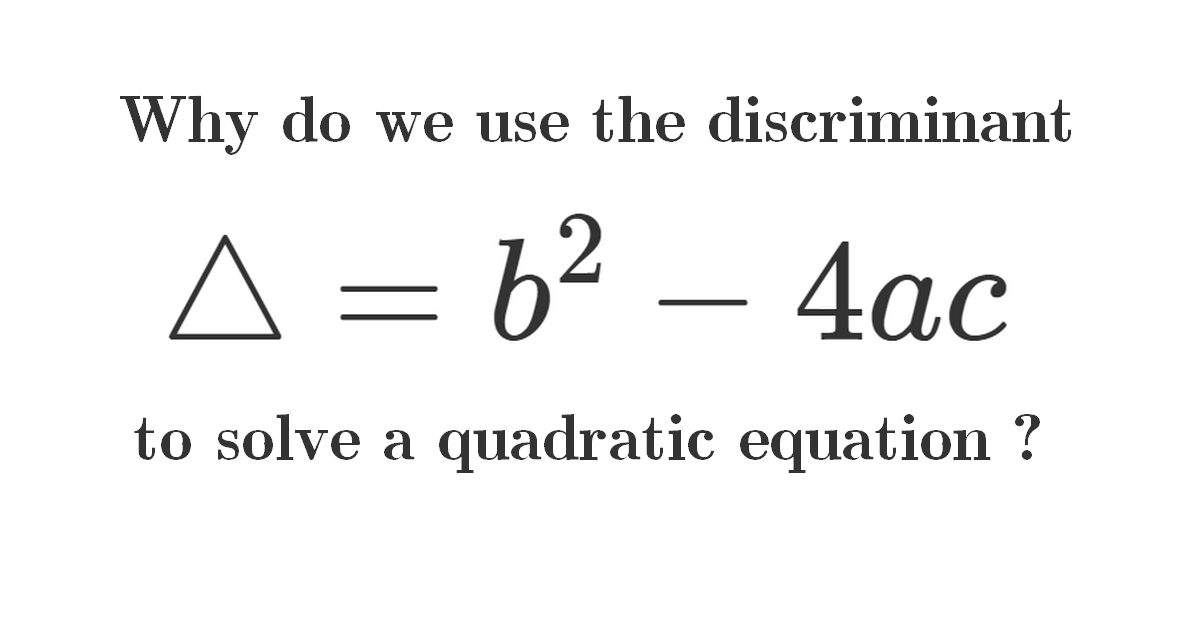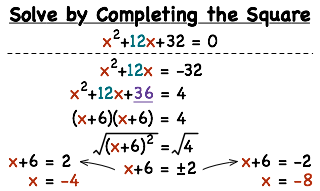Cómo Resolver Ecuaciones Cuadráticas

Comprendiendo las Ecuaciones Cuadráticas

Definición y Forma Estándar (80 Palabras)

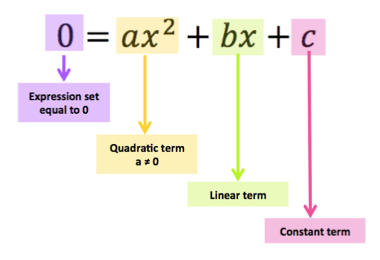
Una ecuación cuadrática es cualquier ecuación que se ajusta a la forma estándar:

\(ax^{2} +bx+c=0\)

Donde:

a, b y c son constantes.

a ≠ 0 (si a = 0, la ecuación se reduce a una lineal).

Una estructura matemática aparentemente sencilla abre puertas a muchas exploraciones fascinantes tanto en las matemáticas como en la realidad. Las raíces de la ecuación pueden tomar la forma de números reales o complejos dependiendo de cómo se implementen en la realidad.

Desglosando los Componentes

Para entender mejor las ecuaciones cuadráticas, desglosaremos sus componentes:

ax²: El coeficiente a determina la curvatura o "ancho" de la parábola. Valores mayores de |a| crean parábolas más empinadas, mientras que valores menores aplanan la curva.

bx: El coeficiente lineal impacta la simetría de la parábola y el desplazamiento horizontal, alterando dónde se encuentra el vértice (punto de inflexión).

c: Los términos constantes representan puntos donde dos líneas se intersectan (x = 0).

Juegan un papel esencial en la forma y posición de las parábolas y proporcionan a los estudiantes métodos adicionales de resolución de problemas relacionados con la geometría para complementar los algebraicos.

Tipos de Ecuaciones Cuadráticas

Las ecuaciones cuadráticas vienen en varias formas:

Cuadráticas Completas

Ecuaciones que contienen todos los términos (\(ax^{2}\) , bx , y c ), como:

\(2x^{2}+3x−5=0\)

Cuadráticas Incompletas

Ecuaciones con términos faltantes, tales como:

Sólo queda el término constante y cuadrado: \(x^{2}-16=0\)

Término constante faltante: \(x^{2}+6x=0\)

Formas Especiales

Estas incluyen variaciones como:

Expresiones factorizables : (x+3)(x−4)=0

Formas expandidas que requieren simplificación, por ejemplo, 3x(x−2)=6

Simplificar ecuaciones cuadráticas incompletas puede acelerar el proceso de resolución para estos casos.

Factorización para Resolver Ecuaciones Cuadráticas

Guía Paso a Paso para Factorizar

La factorización es uno de los métodos más simples e intuitivos para resolver ecuaciones cuadráticas. Sigue estos pasos:

Reorganiza la Ecuación: Asegúrate de que la ecuación esté en forma estándar:

\(ax^{2}+bx+c=0\)

Identifica Factores: Descompón la expresión cuadrática en un producto de dos binomios:

(px+q)(rx+s)=0

Iguala Cada Factor a Cero: Resuelve para x igualando cada binomio por separado a cero:

px+q=0 y rx+s=0

Reconociendo Cuadráticas Factorizables

No todas las ecuaciones cuadráticas son fácilmente factorizables. Sin embargo, muchas presentan patrones reconocibles:

Trinomios Cuadrados Perfectos: Ej., \(x^{2}+6x+9=(x+3)^{2}\).

Raíces Enteras Simples: Coeficientes que permiten una factorización directa, como \(x^{2}+7x+10=(x+5)(x+2)\).

Visión Original: Identificar estos patrones temprano puede ahorrar tiempo y esfuerzo durante el proceso de resolución.

Limitaciones del Método de Factorización

Aunque la factorización es una herramienta poderosa, tiene limitaciones:

Solo funciona cuando la cuadrática es factorizable con raíces racionales.

Raíces complejas o irracionales requieren métodos alternativos, como la fórmula cuadrática o técnicas numéricas.

Usando Enfoques Gráficos con Factorización

Otra forma de aprovechar la factorización implica comprender sus implicaciones gráficas. Una ecuación cuadrática factorizada corresponde a una parábola que intercepta el eje x en sus raíces. Por ejemplo:

(x−2)(x+3)=0

En un gráfico, esto interceptaría en x=2 y x=−3.

Visualizar las intersecciones permite a los estudiantes mejorar sus habilidades de factorización mientras construyen intuición sobre simetría y la ubicación de las raíces.

Resolviendo con la Fórmula Cuadrática

Introducción y Derivación de la Fórmula Cuadrática

La fórmula cuadrática es un enfoque integral para resolver cualquier ecuación cuadrática:

\(x=\frac{-b\pm\sqrt{b^{2}-4ac } }{2a}\)

Se deriva completando el cuadrado para la ecuación cuadrática general:

\(ax^{2}+bx+c=0\)

Divide por a para simplificar.

Reorganiza y completa el cuadrado añadiendo \((\frac{b}{2a} )^{2}\).

Resuelve para x, llegando a la fórmula cuadrática.

En contraste con la factorización, este enfoque proporciona soluciones para cualquier ecuación cuadrática con raíces complejas o raíces no racionales, lo que lo hace invaluable en ecuaciones más difíciles.

Papel del Discriminante (Δ)

El discriminante, \(Δ=b^{2}−4ac\), juega un papel crucial dentro de la fórmula cuadrática, ya que dicta la naturaleza y cantidad de raíces:

Δ>0: Dos raíces reales distintas.

Δ=0: Una raíz (real) repetida.

Δ<0: Dos raíces complejas.

Por ejemplo, considere \(x^{2}−4x+4=0\). Aquí, Δ=0, indicando una raíz repetida, x=2.

Al evaluar Δ temprano, los estudiantes obtienen una idea del comportamiento de la ecuación y pueden planificar su estrategia de solución en consecuencia.

Pasos de Aplicación Práctica

Resolver una ecuación cuadrática usando la fórmula implica:

Identificar coeficientes: a, b, c.

Sustituir en la fórmula:\(x=\frac{-b\pm\sqrt{b^{2}-4ac } }{2a}\)

Simplificar los resultados paso a paso.

Por ejemplo, con \(2x^{2}+3x−2=0\):

a=2,b=3,c=−2.

\(Δ=3^{2}−4(2)(−2)=9+16=25\).

Raíces: \(x=\frac{-3\pm5 }{4}\) ​, dando como resultado x=0.5 y x=−2.

Resolviendo Completando el Cuadrado

¿Qué es Completar el Cuadrado?

El método de completar el cuadrado implica reescribir una ecuación cuadrática en la forma de un trinomio cuadrado perfecto. Esta técnica nos permite expresar la ecuación cuadrática en la siguiente forma estándar:

\((x−h)^{2}=k\)

Aquí, h y k se relacionan con el vértice de la parábola, ofreciendo valiosos conocimientos geométricos. Completar el cuadrado es particularmente útil en situaciones donde el factor común no es posible, al derivar la fórmula cuadrática o en problemas de optimización.

Por ejemplo, resolver una ecuación cuadrática como \(x^{2}+6x+5=0\) usando este método revela las conexiones entre manipulaciones algebraicas y transformaciones parabólicas.

Ejemplo Paso a Paso

Paso 1: Hacer que el Coeficiente de \(x_{2}\)  Sea Igual a 1

Si \(a\ne 1\) en la ecuación estándar \(ax^{2} +bx+c=0\), divide toda la ecuación entre a para normalizar el coeficiente de \(x^{2}\).

Por ejemplo: Resuelve \(2x^{2} +8x−10=0\). Divide entre 2:

\(x^{2} +4x−5=0\)

Paso 2: Sumar y Restar la Mitad del Cuadrado del Coeficiente Lineal

Suma y resta \((\frac{b}{2} ​)^{2}\), el cuadrado de la mitad del coeficiente lineal, para crear un trinomio cuadrado perfecto en el lado izquierdo.

\(x^{2}+4x+(\frac{4}{2} )^{2}−(\frac{4}{2} )^{2}−5=0\)

Simplificar:

\((x+2)^{2}−4−5=0\)

\((x+2)^{2}=9\)

Paso 3: Resolver Usando la Propiedad de la Raíz Cuadrada

Toma la raíz cuadrada de ambos lados:

\(x+2=\pm \sqrt{9}\)

x+2=3 o x+2=−3

Resuelve para x:

x=1 o x=−5

Aplicación de Completar el Cuadrado

Completar el cuadrado está estrechamente ligado a problemas del mundo real, como maximizar ganancias en los negocios, encontrar los valores máximos o mínimos en física y modelar propiedades geométricas.

Entender este método no solo ayuda a resolver ecuaciones, sino que también construye entendimientos sobre problemas de optimización, haciéndolo versátil a través de diversas disciplinas.

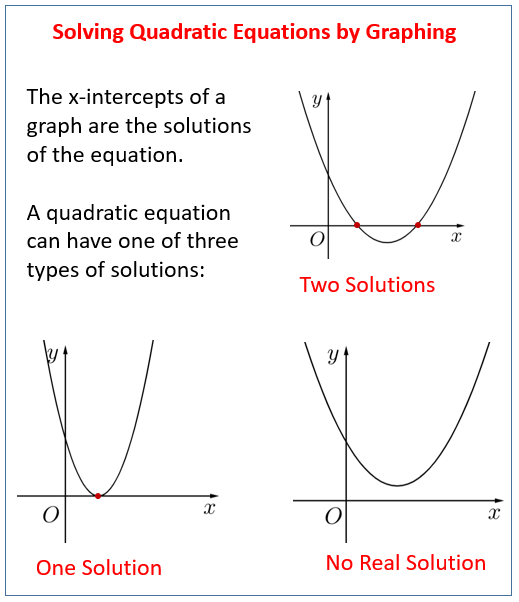
Método Gráfico para Resolver Cuadráticas

Conceptos Básicos de Graficar Cuadráticas

Los métodos gráficos utilizan la representación visual de ecuaciones cuadráticas como parábolas para identificar sus soluciones. Recuerda que la forma general de una ecuación cuadrática, \(y=ax^{2}+bx+c\), produce una parábola cuando se grafica.

Características Clave de la Parábola:

Vértice: El vértice es el punto máximo o mínimo de una parábola, dependiendo de si se abre hacia arriba (a>0) o hacia abajo (a<0).

Eje de Simetría: Una línea vertical que pasa por el vértice, dada por \(x=-\frac{b}{2a}\).

Raíces (Soluciones): Las intersecciones con el eje x donde y=0.

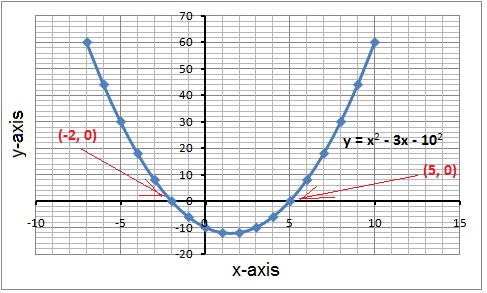
Encontrando Soluciones Usando Gráficas

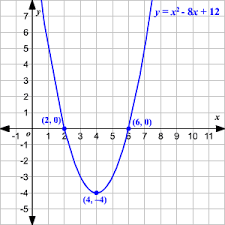
Para resolver una ecuación cuadrática gráficamente, dibuja la parábola correspondiente a \(y=ax^{2}+bx+c\). Las coordenadas x de los puntos donde la parábola cruza el eje x representan las raíces de la ecuación.

Caso 1: Dos Raíces Reales

En el primer caso, donde dos puntos distintos en una parábola cruzan con dos puntos distintos del eje x en dos momentos distintos, esta cuadrática tiene dos soluciones reales (raíces reales).

Caso 2: Una Raíz Repetida

Cuando toca en un solo punto del vértice, solo habrá siempre una solución repetida (Δ=0).

Caso 3: No Hay Raíces Reales

A menos que la parábola interseque el eje x de alguna manera, no hay soluciones reales (Δ<0; estas soluciones deben ser complejas).

Por ejemplo, la ecuación \(x^{2}−4x+3=0\) genera una parábola que intersecta el eje x en x=1 y x=3, correspondientes a las raíces.

Graficar con Herramientas Modernas

Herramientas modernas como Desmos, calculadoras gráficas y bibliotecas de Python simplifican el proceso de visualizar funciones cuadráticas. Estas herramientas proporcionan representaciones visuales precisas, facilitando el análisis de ecuaciones complejas o la aproximación de raíces cuando los métodos algebraicos se complican.

Identificando el Método Más Eficiente para Resolver Ecuaciones Cuadráticas

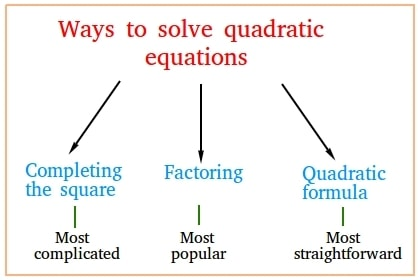
Resumen de los Métodos de Resolución

Diferentes métodos para resolver ecuaciones cuadráticas se adaptan a varios escenarios:

El factoreo puede resolver rápidamente ecuaciones simples con coeficientes pequeños, mientras que la fórmula cuadrática y el completar el cuadrado son soluciones generalmente aplicables. Para transformaciones o problemas con vértices, sin embargo, completar el cuadrado es el enfoque óptimo.

Los métodos gráficos sobresalen ofreciendo visualización y soluciones aproximadas.

Marco de Toma de Decisiones

Seleccionar el mejor método de resolución depende de la complejidad de la ecuación y de tus objetivos:

Paso 1: Comienza con el Factoreo

Si la ecuación es simple y tiene raíces racionales, el factoreo es la opción más rápida.

Paso 2: Verifica el Discriminante Δ

Usa el discriminante para decidir:

Si Δ>0, hay dos raíces reales—considera el factoreo o la fórmula cuadrática.

Si Δ=0, existe una solución, sugiriendo completar el cuadrado o la fórmula cuadrática.

Si Δ<0, las soluciones son complejas; la fórmula cuadrática es la mejor opción.

Paso 3: Usa el Completar el Cuadrado para Análisis de Vértices

Si el problema involucra transformaciones geométricas u optimización (por ejemplo, encontrar un mínimo o máximo), usa completar el cuadrado.

Paso 4: Recurre a Herramientas Gráficas para Aproximación

Para aplicaciones del mundo real o cuando la manipulación algebraica precisa no es viable, utiliza gráficos.

Consejos para Mejorar la Eficiencia

Utiliza verificaciones mentales de factoreo (por ejemplo, reglas de suma-producto) y evaluaciones del discriminante desde el principio al resolver problemas, especialmente en exámenes o durante proyectos de modelado matemático del mundo real. Esto ahorrará tiempo mientras trabajas en ellos rápidamente.

Resolviendo Ecuaciones Usando Métodos Numéricos

¿Por Qué Usar Métodos Numéricos?

Los métodos numéricos se vuelven esenciales cuando las técnicas algebraicas no producen una solución aceptable, como en ecuaciones cuadráticas con raíces complejas que no dan respuestas directas mediante factorización o completando el cuadrado. Cuando esto ocurre, los algoritmos iterativos funcionan eficazmente proporcionando soluciones aproximadas con niveles deseados de precisión.

Los métodos numéricos difieren de los algebraicos en que se centran más en aproximaciones que son prácticamente útiles que en soluciones exactas, lo que hace que estas técnicas sean adecuadas para aplicaciones de modelado computacional en ingeniería, física computacional y aplicaciones de pronóstico financiero.

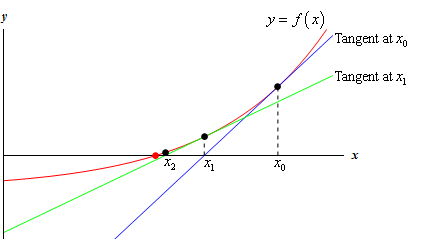
Ejemplo Detallado de Solución Iterativa

Uno de los métodos numéricos más utilizados es el Método de Newton para resolver ecuaciones. Para una ecuación cuadrática como \(f(x)=ax^{2}+bx+c=0\), el Método de Newton sigue esta fórmula iterativa:

\(x_{n+1} ​=x_{n} ​−\frac{f(x_{n})}{f{}'(x_{n}) }\)

Paso 1: Elegir una Suposición Inicial

Comience estimando un valor aproximado para la raíz (x_{0}​) cerca de donde la ecuación podría igualar cero.

Paso 2: Aplicar la Fórmula Iterativa

Calcule puntos subsiguientes (\(x_{n+1}\)​) usando \(x_{n}\)​ y evalúe f(x) y su derivada \({f}' (x)\).

Por ejemplo, resolviendo \(f(x)=x^{2}−2=0\):

Comience con \(x_{0}​=1.5\).

Primera iteración:

\(x_{1}​=1.5−\frac{1.5^{2}-2 }{2(1.5)} =1.41667\)

Repita hasta la convergencia.

Paso 3: Determinar la Convergencia

Continúe las iteraciones hasta que x_{n}​ se estabilice, indicando la aproximación de una raíz.

Aplicaciones del Mundo Real de las Ecuaciones Cuadráticas

Cuadráticas en Física

Las ecuaciones cuadráticas son una piedra angular de la física moderna, proporcionando modelos de muchos fenómenos naturales:

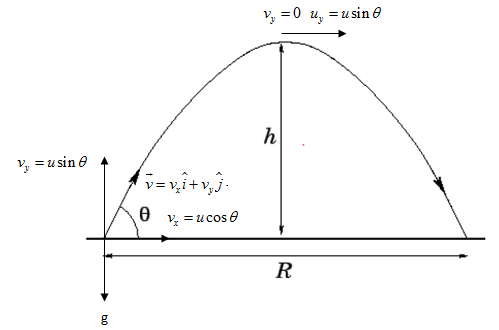
Movimiento de Proyectiles: La altura del proyectil es un concepto esencial en balística y física del deporte, determinado al resolver esta cuadrática: \(h(t)=−\frac{1}{2} ​gt^{2}+v_{0}​t+h_{0}\). Resolver esta cuadrática revelará cuándo un objeto alcanza la altura máxima o toca el suelo, proporcionándonos estimaciones de tiempo. Por ejemplo, resolverla revela cuándo alcanza la altura máxima o toca fondo.

Óptica: Las ecuaciones cuadráticas utilizadas en el diseño óptico describen espejos y lentes parabólicos, siendo su creación esencial en el desarrollo de telescopios, cámaras y láseres. Al resolver tales ecuaciones, los científicos pueden predecir trayectorias con precisión, optimizar dispositivos y simular interacciones físicas necesarias para la innovación tecnológica.

Problemas Económicos y de Optimización

Las ecuaciones cuadráticas juegan un papel crítico en la economía y optimización de recursos:

Maximización de Beneficios: Las cuadráticas modelan curvas de ingresos y costos, permitiendo a las empresas encontrar precios o valores de producción que maximizan las ganancias. Por ejemplo, si la ganancia se expresa como \(P(x)=−x^{2}+50x−200\), resolver la ecuación optimiza la producción.

Las ecuaciones cuadráticas desempeñan un papel invaluable en la optimización de problemas en todas las industrias proporcionando una asignación eficiente de recursos, reducción de costos y eficiencias operativas, convirtiéndose así en una herramienta esencial.

Conclusión

El dominio de las ecuaciones cuadráticas construye una base sólida no solo en álgebra sino también en el pensamiento analítico. Ya sea a través del factoreo, completando el cuadrado, utilizando la fórmula cuadrática, o confiando en métodos gráficos o numéricos, cada enfoque tiene sus propios puntos fuertes.

Al explorar estas técnicas a fondo, estudiantes y profesionales pueden resolver con confianza diversos problemas matemáticos y aplicar su conocimiento en distintas disciplinas.

Referencia:

https://tutorial.math.lamar.edu/classes/calci/newtonsmethod.aspx

https://www.ga-ccri.com/can-a-neural-net-learn-the-quadratic-formula

https://github.com/aditeyabaral/gpython