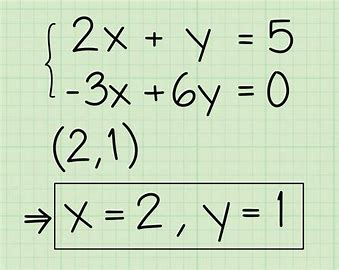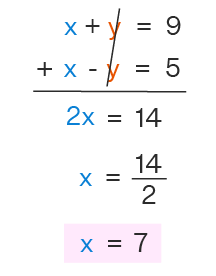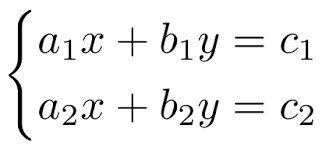Cómo Resolver un Sistema de Ecuaciones

¿Qué es un sistema de ecuaciones?

Definición

En esencia, un sistema de ecuaciones se refiere a cualquier conjunto de dos o más ecuaciones algebraicas que involucran variables similares y que deben cumplirse simultáneamente. Al resolver tales sistemas de ecuaciones, el objetivo debe ser encontrar los valores de las variables que hagan verdaderas todas las ecuaciones. Para un ejemplo simultáneo, considere el siguiente sistema de dos ecuaciones:

x+y=10 y x−y=4

Aquí, las variables x e y se comparten en ambas ecuaciones. La solución de este sistema es x=7 e y=3, ya que estos valores satisfacen ambas ecuaciones cuando se sustituyen.

Importancia

Los sistemas de ecuaciones están en el núcleo del álgebra porque nos permiten resolver relaciones entre múltiples cantidades y cantidades que dependen unas de otras. Son más que ideas abstractas: los sistemas de ecuaciones proporcionan tareas prácticas como la asignación de recursos o la determinación de fuerzas sobre un objeto al dominar técnicas para resolverlos eficazmente y aplicar nuestro conocimiento en muchas áreas que requieren optimización o resolución de problemas.

Tipos de Sistemas de Ecuaciones

Los sistemas de ecuaciones pueden clasificarse de múltiples maneras, principalmente basándose en el número de soluciones y el tipo de ecuaciones involucradas.

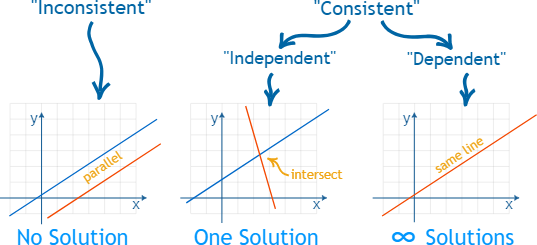
Clasificaciones Basadas en el Número de Soluciones

Solución Única

Un sistema de ecuaciones tiene una solución única cuando hay exactamente un conjunto de valores de variables que satisface todas las ecuaciones. Por ejemplo:

2x+y=6 y x−y=2

Gráficamente, esto corresponde a dos líneas que se cruzan en un solo punto x=2,y=2. Las soluciones únicas son críticas en la modelación de problemas con restricciones fijas, como el presupuesto dentro de un límite financiero específico.

Sin Solución

Un sistema sin una solución obvia a menudo resulta cuando todas sus ecuaciones representan líneas paralelas que nunca se cruzan; simplemente no puede haber valores que hagan que todas las ecuaciones sean verdaderas al mismo tiempo. Por ejemplo:

x+y=3 y x+y=5

Estas líneas son paralelas y distintas, lo que indica que el sistema no tiene solución.

Soluciones Infinitas

Cuando un sistema tiene infinitas soluciones, las ecuaciones esencialmente describen la misma línea. Por ejemplo:

x+y=3 y 2x+2y=6

Ambas ecuaciones representan una línea, y cada punto en ella representa una solución para el sistema. Tales instancias se presentan en escenarios con restricciones redundantes o información incompleta entre ellas.

Sistemas Lineales vs. No Lineales

Sistemas Lineales

Los sistemas lineales son sistemas en los cuales todas las ecuaciones son lineales, lo que significa que forman líneas rectas en un gráfico bidimensional. Tales sistemas toman la forma general:

Ax+By=C

Los sistemas lineales son cruciales porque sus soluciones pueden resolverse de manera confiable y rápida mediante sustitución, eliminación o matrices.

Sistemas No Lineales

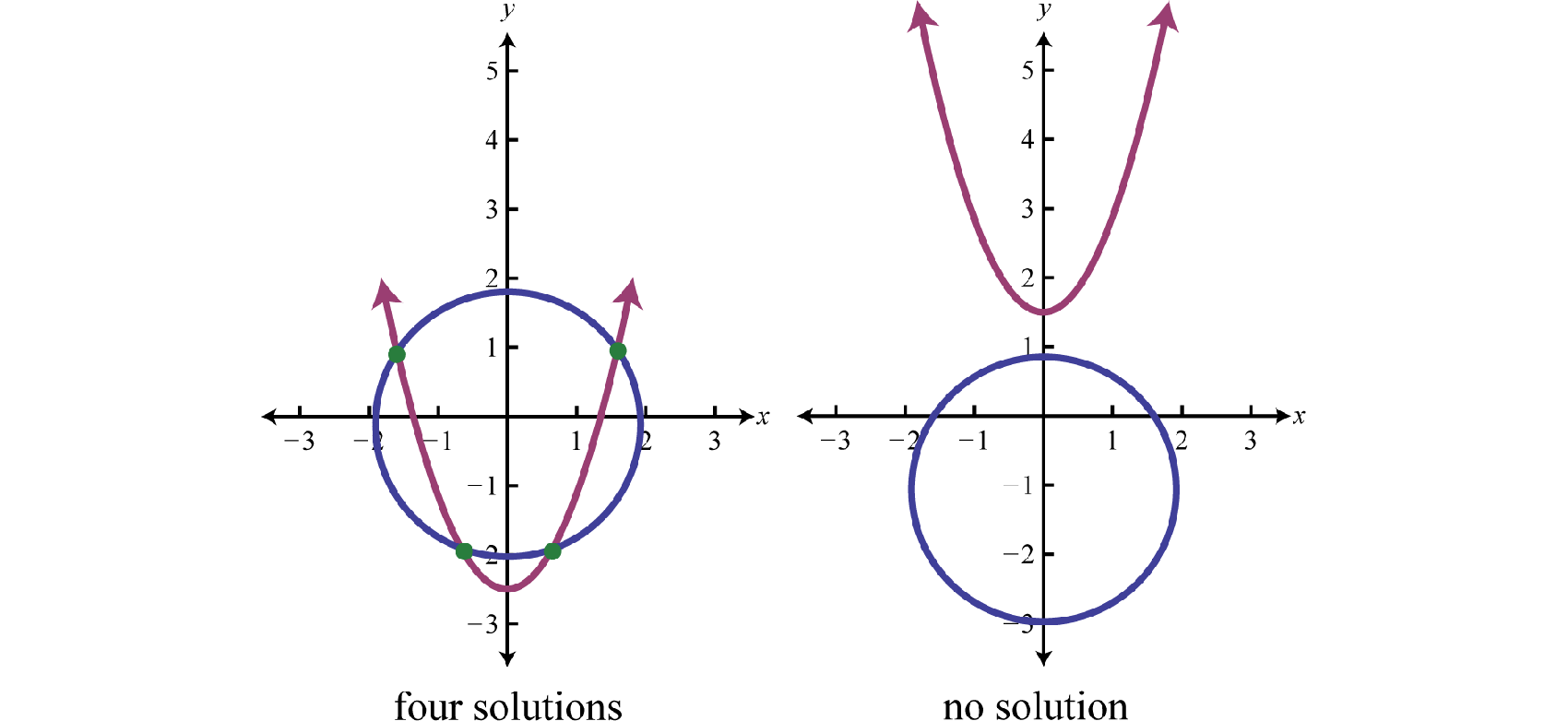
Los sistemas no lineales, por otro lado, involucran al menos una ecuación que no es lineal, estas pueden involucrar exponentes, raíces u otras relaciones complejas. Por ejemplo:

\(x^{2} + y^{2} =25\) y y=2x

Estas ecuaciones representan un círculo y una línea, respectivamente. Resolver sistemas no lineales a menudo requiere métodos numéricos, como el método de Newton o aproximación iterativa. Los sistemas no lineales son más desafiantes porque las relaciones entre variables son más complejas, y las soluciones pueden involucrar múltiples intersecciones o ninguna intersección en absoluto.

Métodos para Resolver Sistemas de Ecuaciones

Ahora que entendemos qué son los sistemas de ecuaciones y los tipos de soluciones que pueden tener, exploremos técnicas detalladas para resolverlos.

Método de Sustitución

El método de sustitución consiste en aislar una variable en una ecuación y sustituir esa expresión en la otra ecuación para reducirla a una ecuación de una sola variable.

Paso 1: Aislar una Variable

Seleccione una ecuación y aísle una variable expresándola en términos de la otra. Por ejemplo, de la ecuación y=2x+1, y ha sido aislada en términos de x.

Paso 2: Sustituir en la Segunda Ecuación

Reemplace esta expresión para y en la segunda ecuación. Por ejemplo, si la segunda ecuación es x+y=7, sustituya y=2x+1 para obtener:

x+(2x+1)=7

Paso 3: Resolver la Ecuación de una Sola Variable

Simplifique la ecuación para resolver x:

3x+1=7⟹3x=6⟹x=2

Paso 4: Sustitución Inversa

Inserte x=2 en la primera ecuación para resolver y:

y=2(2)+1=5

Paso 5: Verificar la Solución

Inserte x=2 y y=5 en las ecuaciones iniciales para verificar la solución.

x+y=7⟹2+5=7,y y=2x+1⟹5=4+1

Así, la solución es x=2,y=5. La sustitución es más efectiva cuando una de las ecuaciones ya está parcialmente resuelta para una variable.

Método de Eliminación

El método de eliminación es un enfoque eficiente para resolver sistemas de ecuaciones al cancelar una variable.

Paso 1: Ajustar los Coeficientes

Multiplique una o ambas ecuaciones para que los coeficientes de una variable sean iguales en magnitud pero opuestos en signo. Por ejemplo, considere las ecuaciones:

2x+3y=12 y 4x−y=10

Multiplique la segunda ecuación por 3 para igualar los coeficientes de y:

2x+3y=12 y 12x−3y=30

Paso 2: Sumar o Restar

Sume las dos ecuaciones para eliminar y:

(2x+3y)+(12x−3y)=12+30⟹14x=42

Resolver da x=3.

Paso 3: Resolver la Variable Restante

Sustituya x=3 en la primera ecuación:

2(3)+3y=12⟹6+3y=12⟹3y=6⟹y=2

Paso 4: Verificar la Solución

Siempre verifique la solución en ambas ecuaciones originales para asegurar la precisión. La solución para este sistema es x=3,y=2.

Consejo: Busque coeficientes que se puedan escalar fácilmente (por ejemplo, dobles, triples) para agilizar el proceso de eliminación.

Método Gráfico

El método gráfico implica trazar cada ecuación en un plano de coordenadas e identificar sus puntos de intersección. Este método proporciona una comprensión intuitiva y visual del sistema.

Pasos

Convierta todas las ecuaciones a la forma de pendiente-intercepto (y=mx+b).

Por ejemplo, 2x+y=6 se convierte en y=−2x+6.

Trace cada ecuación en un plano de coordenadas. La pendiente (m) determina la inclinación de la línea, y el intercepto en y (b) determina dónde cruza el eje y.

Identifique el o los puntos de intersección, que representan la o las soluciones al sistema.

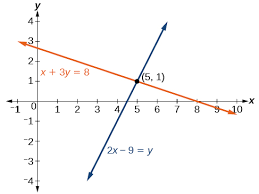
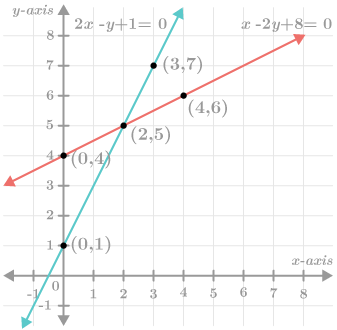
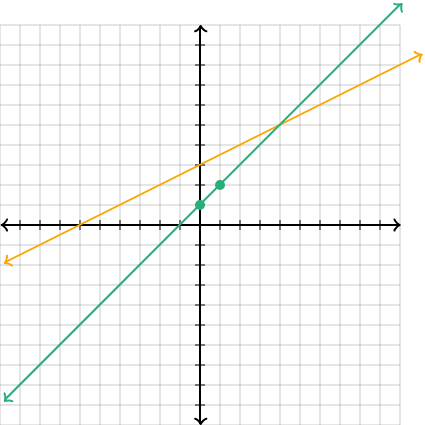
Ejemplo

Para y=−2x+6 y y=\frac{1}{2} x+3, al graficar se verá que las líneas se intersectan en x=2,y=4. Esta es la solución del sistema.

Método de Cruzado

Definición

El método de cruzado proporciona un enfoque indirecto y basado en fórmulas para resolver sistemas de dos ecuaciones lineales con dos incógnitas. Evita cálculos paso a paso aplicando directamente fórmulas derivadas de la matriz determinante como reglas prácticas directas.

Pasos

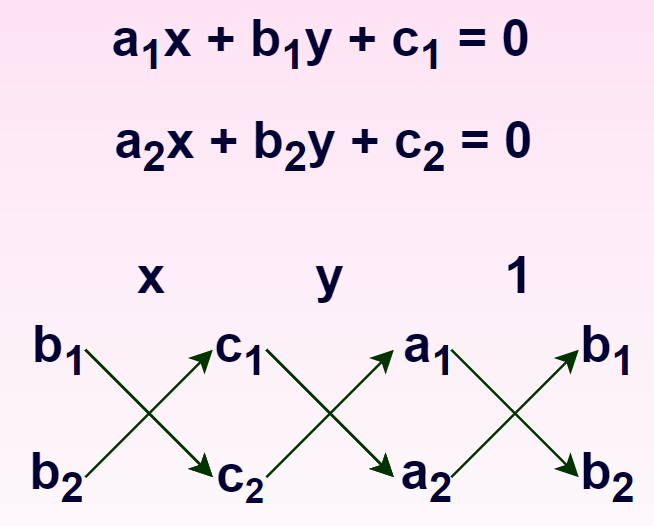
Para dos ecuaciones:

\(m_{1} ​x+n_{1} ​y+p_{1} = 0\) y \(m_{2} x+n_{2} ​y+p_{2} = 0\)

Las fórmulas para resolver x e y son:

\(x/(n_{1}​ p_{2}​−n_{2}​ p_{1}​)=−y/(m_{1}​ p_{2}​​−m_{2}​ p_{1}​​)=1/(m_{1}​ n_{2}​−m_{2}​ n_{1}​)\)

Resolver x usando:

\(x=(n_{1}​ p_{2}−n_{2} ​p_{1}​) / (m_{1}​ n_{2}​−m_{2} ​n_{1}​)\)

Resolver y usando:

\(y=(p_{1}​ m_{2}​−p_{2}​ m_{1}​)/(m_{1}​ n_{2}​−m_{2}​ n_{1}​)\)

Ejemplo de Metodología

Para las ecuaciones:

x+y=5 y 2x−3y+7=0

Con coeficientes \(a_{1} =1, b_{1} =1, c_{1} ​=−5\) y \(a_{2} ​=2, b_{2} ​=−3, c_{2} ​=−7\), use las fórmulas anteriores para calcular x e y. Este método es efectivo cuando las ecuaciones están explícitamente representadas en forma estándar.

Método Matricial

Definición

El método matricial proporciona un enfoque universal para resolver sistemas de ecuaciones lineales, especialmente en dimensiones superiores. El sistema de ecuaciones se reescribe en la forma AX=B, donde:

A=Matriz de Coeficientes,X=Matriz de Variables,B=Matriz de Constantes.

Por ejemplo, el sistema:

2x+3y=6 y x−2y=3

puede escribirse como:

\(\begin{bmatrix} 2& 3\\ 1 &-2\end{bmatrix} \begin{bmatrix} x\\y\end{bmatrix}=\begin{bmatrix} 6\\3\end{bmatrix}\)

Pasos

Exprese el Sistema en Forma Matricial

Use AX=B, donde A es la matriz de coeficientes, X es la matriz columna de variables, y B es la matriz columna de constantes.

Encuentre la Inversa de la Matriz de Coeficientes A:

Calcule \(A^{-1}\) :

\(A^{-1} = \frac{1}{det(A)} ​\begin{bmatrix} d & -b\\ -c&a\end{bmatrix}\)

Para sistemas donde\(det(A) \ne\) 0, calcule \(X=A^{-1}B\).

Resolver Variables: Use la multiplicación de matrices para calcular X, dando los valores de x e y.

Aptitud de Cada Método

Cada método para resolver sistemas tiene sus propias fortalezas y es mejor usarlo en ciertas circunstancias:

Método de Sustitución: La sustitución puede reducir rápidamente un problema de dos variables a una ecuación de solo una variable al reemplazar rápidamente una variable con las otras y resolverlas todas al mismo tiempo. Por ejemplo, con la ecuación y=2x+3, se torna fácil combinar estas en un problema de una sola variable a través de la sustitución.

Método de Eliminación: La eliminación puede ser más eficaz cuando los coeficientes pueden alinearse o alterarse rápida y fácilmente para alcanzar el equilibrio; por ejemplo, sistemas como 2x+5y=12 y 4x+5y=20 son candidatos ideales ya que sus términos y se cancelan tras la resta, haciendo que la eliminación sea una solución atractiva.

Método Gráfico: Proporciona una comprensión visual de las soluciones, pero puede volverse inaplicable cuando se trata de sistemas complejos que implican decimales o fracciones.

Método de Matrices: Ideal para sistemas grandes que involucran tres o más variables, el enfoque de matrices ayuda a abordar problemas de manera organizada y eficiente.

Marco de Decisión Original

Al elegir un método, considere:

Estructura del Sistema

Busque simetrías o formas simplificadas.

Si una variable ya tiene coeficientes iguales, use eliminación.

Si una variable puede aislarse fácilmente, opte por sustitución.

Tamaño del Sistema

Para sistemas pequeños, los métodos manuales (sustitución/eliminación) funcionan bien; para los más grandes, confíe en matrices o solucionadores numéricos.

Requerimiento de Precisión

Si se necesitan soluciones exactas, evite los métodos gráficos a menos que cuente con herramientas de software.

Errores Comunes y Cómo Evitarlos

Errores Aritméticos y Algebraicos

Un problema común al resolver sistemas de ecuaciones son los simples errores aritméticos, como manejar incorrectamente los signos durante la suma o resta, olvidar distribuir un coeficiente, o manejar mal las fracciones.

Solución

Para evitar errores, escriba todos los pasos claramente y verifique los cálculos en cada etapa. Por ejemplo, al resolver:

2x+3y=6 y 4x−y=10

asegúrese de tratar consistentemente con los signos: multiplicar una ecuación por -1 debe afectar a toda la ecuación.

Errores al Graficar

Al trazar líneas o determinar un punto de intersección usando técnicas de graficación, puede haber margen de error al graficar y crear soluciones; incluso pequeñas imprecisiones pueden llevar a que se presenten soluciones incorrectas como respuestas.

Remedio

Siempre use calculadoras graficadoras o software como Desmos o Microsoft Excel al visualizar sistemas. Un gráfico trazado puede revelar si las líneas se intersectan, son paralelas o se superponen completamente, ofreciendo conocimientos más allá de coordenadas precisas.

Errores en Soluciones Matriciales

El método de matrices presenta dificultades especiales, particularmente para matrices casi singulares cuyo det(A) se acerca a cero; producen inversas poco fiables y, por lo tanto, hacen que el sistema no sea viable para su uso.

Solución

Pueden ser necesarios métodos numéricos o técnicas iterativas. Además, verifique valores de determinantes cercanos a cero. Use herramientas computacionales como NumPy (Python) que automáticamente señalan cualquier matriz mal condicionada.

Técnicas Avanzadas para Sistemas Complejos

Métodos Numéricos Iterativos

Para sistemas no lineales o de gran escala, los métodos iterativos como el Método de Newton-Raphson o el Método de Gauss-Seidel son útiles. Estos enfoques aproximan soluciones repetidamente para mejorar la precisión.

Método de Gauss-Seidel

Este método iterativo resuelve una variable a la vez usando aproximaciones de iteraciones anteriores, refinando continuamente las estimaciones.

Método de Newton para Sistemas No Lineales

Si su sistema contiene ecuaciones como \(x^{2} + y^{2} =25\) y y=2x, el Método de Newton emplea derivadas para buscar soluciones aproximadas iterativamente.

Estas técnicas pueden requerir gran poder de cómputo pero son indispensables al abordar problemas de ingeniería y física con soluciones complejas que no pueden ser fácilmente expresadas usando lenguajes simples.

Uso Mejorado de la Tecnología

La tecnología moderna juega un papel esencial en la resolución de sistemas complejos. Bibliotecas de Python como SymPy y NumPy ofrecen computación en tiempo real incluso para sistemas grandes; herramientas como MATLAB pueden manejar matrices, ejecutar métodos iterativos y construir gráficos visuales tridimensionales para una visualización aún mayor de conjuntos de datos.

Aplicaciones en la Vida Real

Dominios Clave

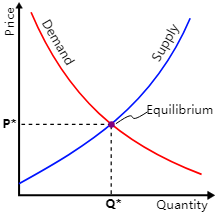
Economía 

Los sistemas de ecuaciones modelan curvas de oferta y demanda, presupuestos y problemas de optimización. Por ejemplo, encontrar el precio de equilibrio en un mercado requiere resolver dos ecuaciones de demanda y oferta.

Física

Resolver fuerzas en sistemas mecánicos, tal como lo describen las leyes de Newton. Por ejemplo, un sistema que involucra F=ma y v=u+at relaciona fuerza, masa y aceleración con la velocidad.

Negocios y Logística

Los sistemas se utilizan frecuentemente para optimizar horarios de producción, minimizar gastos y asignar recursos.

Marco de Modelado de Problemas

Definir Variables

Comienza identificando qué representan x, y y otras variables en el problema.

Establecer el Sistema

Escribe ecuaciones que capturen las restricciones del problema.

Seleccionar un Método

Elige un método de solución basado en la complejidad del problema (por ejemplo, sistemas pequeños: sustitución; sistemas grandes: enfoques matriciales/numericos).

Verificar la Solución

Asegúrate de que los resultados se alineen con las restricciones del mundo real e interpreta los resultados de manera significativa.

Conclusión

Resolver sistemas de ecuaciones es una habilidad esencial con diversas aplicaciones en campos como la economía, la ingeniería y la física. Al entender los diferentes tipos de sistemas (únicos o ninguno) con soluciones--ninguna o infinita--y usando métodos apropiados como sustitución o eliminación para llegar a soluciones únicas o ninguna lo más rápido y preciso posible usando herramientas computacionales modernas como NumPy de Python o MATLAB, podemos asegurar precisión y eficiencia incluso para sistemas complejos o no lineales; los sistemas de ecuaciones nos brindan una forma poderosa de modelar escenarios del mundo real permitiéndonos analizar relaciones, optimizar decisiones más confiadamente mientras resolvemos desafíos prácticos con facilidad.

Referencia：

https://www.simplilearn.com/tutorials/excel-tutorial/data-analysis-excel

https://www.mdpi.com/2078-2489/11/4/193

https://www.statology.org/predictions-regression/