¿Qué es el Álgebra Lineal?

El álgebra lineal, como una rama importante de las matemáticas, explora vectores, matrices y mapeos lineales así como soluciones de sistemas lineales. Imagina planear una salida donde el transporte, las comidas y el alojamiento deben ser coordinados - esto requiere encontrar un equilibrio equitativo entre múltiples variables; el álgebra lineal nos ayuda a comprender y abordar situaciones tan complejas resolviendo ecuaciones de esta forma. Por ejemplo, podrías usar sistemas de ecuaciones de la forma Ax = b. Donde la matriz A representa relaciones entre varios factores, y los vectores x y b representan requerimientos numéricos específicos, respectivamente.

En este artículo, cubriremos gradualmente las definiciones esenciales, las principales ramas, algoritmos numéricos y aplicaciones interdisciplinarias del álgebra lineal. A través de ejemplos de la vida real y fórmulas intuitivas, nuestro objetivo es ayudar a los lectores a captar su esencia fundamental mientras aumentan sus habilidades prácticas para resolver problemas - ya sean estudiantes, ingenieros o científicos de datos! - el álgebra lineal se convertirá en una herramienta imprescindible.

Fundamentos y Definiciones de Álgebra Lineal

Definiciones y Conceptos Básicos de Álgebra Lineal  

Vectores, Matrices y Funciones Lineales  

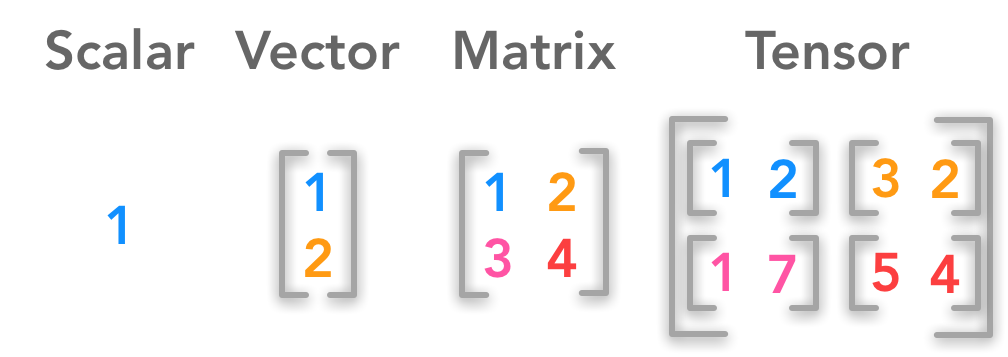
En el núcleo del álgebra lineal se encuentra un concepto abstracto conocido como vector, que no solo sirve para representar un segmento de línea dirigido en el espacio, sino también como una herramienta esencial para describir cantidades y direcciones. Los vectores se representan comúnmente con su abreviatura \(\vec{v}\), con todos los vectores perteneciendo a cualquier conjunto cerrado bajo operaciones de adición y multiplicación. Una matriz representa datos así como transformaciones con su forma determinada por filas y columnas que componen su representación matricial.

\(A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}\) 

Basándose en la relación entre matrices y vectores, las funciones lineales (o transformaciones lineales) pueden definirse matemáticamente como mapeos que satisfacen dos condiciones \(f: V \rightarrow W\) que satisfacen:  

\(f(c_1 \vec{v}_1+c_2 \vec{v}_2)=c_1 f(\vec{v}_1)+c_2 f(\vec{v}_2),\)  

El álgebra lineal proporciona a ingenieros y científicos por igual una herramienta que convierte relaciones de datos complejas en fórmulas operativas manejables, proporcionando apoyo teórico para resolver problemas difíciles relacionados con la ingeniería y la ciencia.

Ecuaciones Lineales y Sus Soluciones  

Las ecuaciones matriciales se encuentran entre los modelos matemáticos más frecuentemente empleados para sistemas lineales, incluyendo:

\(Ax=b,\) (u otras fórmulas similares).

Donde \(A\) representa la matriz de coeficientes, \(x\) es un vector desconocido, y \(b\) representa un vector constante. Existen varias soluciones para resolver tales sistemas de ecuaciones, incluyendo eliminación gaussiana, inversión de matrices y métodos iterativos; la eliminación gaussiana tiene su idea central en usar operaciones elementales de fila para transformar matrices de coeficientes a una forma triangular superior y gradualmente resolver hacia atrás las incógnitas a lo largo del tiempo. Si la matriz \(A\) es no singular, su solución puede expresarse como

\(x=A^{-1}b.\)   

Esto no solo ilustra su unicidad, sino que también enfatiza cuán importantes pueden ser las operaciones matriciales cuando se aplican prácticamente, ayudándonos a comprender mejor fenómenos complejos.

Espacios Vectoriales  

Propiedades de los Espacios Vectoriales y Subespacios  

Los espacios vectoriales son conceptos esenciales en la teoría de conjuntos, definidos como conjuntos que contienen vectores junto con operaciones de adición y multiplicación que satisfacen ocho axiomas fundamentales. Estos axiomas aseguran que cualquier suma o producto entre vectores dentro de un espacio aún pertenezca a ese mismo espacio, y cualquier combinación de vector y escalar permanezca dentro de ese mismo espacio; un ejemplo serían todos los \(n\)-vectores dimensionales sobre el campo de los números reales \(\mathbb{R}\) formando uno de esos espacios. Los subespacios en los espacios vectoriales a menudo sirven para simplificar el análisis de problemas al mismo tiempo que dan una idea de su estructura a través de conceptos como base y dimensión. Los subespacios no solo ayudan a la resolución de problemas, sino que pueden proporcionar datos estructurales invaluables mediante propiedades de cierre como la adición y la multiplicación.

Mapeos Lineales e Independencia Lineal  

Un puente importante para vincular espacios vectoriales es el mapeo lineal, que cumple con su propiedad de mapeo:

\(T(c_1 \vec{v}_1+c_2 \vec{v}_2)=c_1 T(\vec{v}_1)+c_2 T(\vec{v}_2).\)  

Esta propiedad de independencia lineal nos permite modelar con precisión procesos de mapeo utilizando matrices y analizar cómo la transformación afecta la estructura del espacio. Por otro lado, la independencia lineal sirve como criterio esencial para establecer si los vectores pueden formar una base. Si un conjunto de vectores \(\{\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_k\}\) satisface  

\(c_1\vec{v}_1+c_2\vec{v}_2+\cdots+c_k\vec{v}_k=0 \Rightarrow c_1=c_2=\cdots=c_k=0,\)  

Entonces, este conjunto de vectores se dice que es linealmente independiente; esta propiedad les permite formar la base y determinar la dimensión de un espacio vectorial.

Ramas del Álgebra Lineal

Álgebra Lineal Elemental  

Operaciones Básicas de Matrices y Resolución de Sistemas Lineales  

El álgebra lineal elemental enfatiza las operaciones básicas de matrices y sus aplicaciones para resolver sistemas de ecuaciones lineales, considerando la suma, multiplicación, transposición y multiplicación, entre otras, como operaciones clave del álgebra lineal elemental. Una matriz \(A\) y una matriz \(B\) se definirían típicamente por:

\((AB)_{ij}=\sum_{k=1}^{n} a_{ik}\, b_{kj},\)  

donde \(a_{ik}\) y \(b_{kj}\) son los elementos de la \(i\)ª fila \(k\)ª columna de la matriz \(A\) y la \(k\)ª fila \(j\)ª columna de la matriz \(B\), respectivamente. Tales operaciones nos permiten describir relaciones de mapeo en combinatoria así como procesos de transformación con datos.

La eliminación gaussiana es una técnica extremadamente útil al resolver sistemas de ecuaciones lineales; este enfoque aplica una serie de transformaciones elementales para convertir una matriz de ecuaciones en una forma triangular superior o en escalera antes de que se pueda utilizar la sustitución regresiva para completar cualquier desconocido. Considere un caso en el que necesite resolver múltiples sistemas lineales simultáneamente usando esta estrategia:

\(Ax=b,\)  

Donde \(A\) representa la matriz de coeficientes y \(b\) el vector constante, empleando operaciones elementales de filas, podemos transformar la matriz \(A\) en una matriz triangular superior \(U\), produciendo así un vector constante intermedio llamado \(c\), resolviendo gradualmente el vector \(x\). Cuando la matriz \(A\) es no singular, su solución única puede expresarse utilizando notaciones simbólicas:

\(x=A^{-1}b.\)  

Mientras que el método de la matriz inversa es relativamente rápido y económico de computar, su costo computacional puede ser costoso; por lo tanto, la eliminación gaussiana se ha vuelto popular como técnica matemática para profundizar nuestra comprensión de las estructuras matriciales así como para proporcionar una base sólida para cálculos de ingeniería y científicos.

Álgebra Lineal Avanzada  

Valores Propios, Vectores Propios y Descomposición en Valores Singulares  

El álgebra lineal avanzada profundiza en los análisis de matrices, incluyendo valores propios, vectores propios y descomposición en valores singulares (SVD). Para una matriz \(n \times n\) \(A\), si existe un vector no nulo \(x\) y un escalar \(\lambda\) tal que  

\(Ax=\lambda x,\)  

Una vez identificado, un valor propio de \(A\) puede ser representado como un número entero llamado \(\lambda\), y su respectivo vector propio a menudo se conoce como \(x\). Para resolver un problema de valores propios, uno típicamente calcula su determinante.

\(A-\lambda I,\)  

y luego resuelve la ecuación característica  

\(\det(A-\lambda I)=0,\)  

Un cálculo exhaustivo de valores propios permite conocer todos los posibles valores propios de cualquier matriz. Está íntimamente relacionado con cuestiones de estabilidad del sistema y modos vibracionales en problemas de ingeniería e investigación científica.

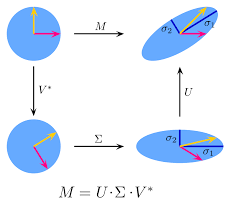
La Descomposición en Valores Singulares (SVD) es un método avanzado de descomposición de matrices que expresa cualquier matriz como el producto de tres matrices. Más precisamente, para cualquier matriz \(m \times n\) \(A\), existe una matriz ortogonal \(U\) y \(V\), así como una matriz diagonal \(\Sigma\), tal que  

\(A=U\Sigma V^{T},\)  

SVD no solo establece teóricamente la universalidad de la descomposición de matrices, sino que también se aplica ampliamente en el procesamiento de señales, compresión de datos y proyectos de ingeniería para reducir dimensionalidad y reducción de dimensión.

La capacidad del álgebra lineal avanzada para revelar la estructura espectral inherente en matrices nos ayuda a apreciar e interpretar más plenamente las características esenciales de los datos. Las técnicas de descomposición como la Descomposición en Valores Propios o la Descomposición en Valores Singulares ofrecen métodos poderosos para resolver problemas complejos relacionados con el análisis de grandes datos, procesamiento de imágenes y aprendizaje automático.

Álgebra Lineal Numérica y Aplicada

Algoritmos Numéricos

Método de Eliminación Gaussiana

Los algoritmos numéricos, un componente integral de las matemáticas computacionales modernas, sirven para resolver modelos de álgebra lineal encontrados en la práctica usando soluciones numéricas aproximadas. La eliminación gaussiana, uno de esos algoritmos de eliminación en n dimensiones, funciona empleando operaciones elementales en las partes triangulares inferiores de matrices para eliminar elementos en la parte triangular inferior y así transformar el sistema de ecuaciones lineales a forma triangular superior, por ejemplo, para una ilustración, considere este sistema lineal representado como:

\(Ax=b,\)  

A través de una secuencia de operaciones elementales de fila, la matriz \(A\) se puede convertir en una matriz triangular superior \(U\)y resultar en un sistema equivalente.

\(Ux=c.\)  

La sustitución hacia atrás puede entonces emplearse comenzando con la fila final para calcular secuencialmente valores aproximados de las variables desconocidas. Aunque altamente efectivo para resolver problemas de pequeña y mediana escala, su inestabilidad numérica podría volverse problemática cuando se trabaja en problemas grandes que requieren altas dimensiones y muchas incógnitas que requieren soluciones aproximadas; métodos más estables como la descomposición QR pueden por lo tanto ser más adecuados en estos casos.

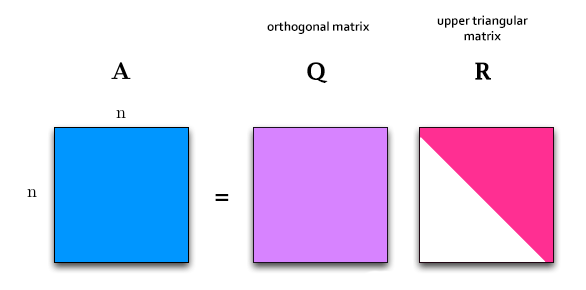
Descomposición QR y Métodos Iterativos

La descomposición QR es una técnica que descompone una matriz en el producto de una matriz ortogonal \(Q\) y una matriz triangular superior \(R\), es decir,  

\(A=QR,\)  

donde la matriz ortogonal \(Q\) satisface  

\(Q^TQ=I,\)  

Y \(R\) es una matriz triangular superior. La descomposición QR puede utilizarse no solo para resolver sistemas lineales sino que también se aplica ampliamente en encontrar soluciones numéricas a problemas de mínimos cuadrados y de valores propios. Al resolver problemas de mínimos cuadrados, el objetivo debería ser localizar un vector \(x\) que minimice la norma del error.

\(\|Ax-b\|_2,\)  

Y al utilizar la descomposición QR, el sistema puede transformarse en  

\(Rx=Q^Tb,\)  

Permitiendo una rápida solución a través de sustitución hacia atrás.

Además, los métodos numéricos iterativos (como los métodos de Jacobi y de Gauss-Seidel) proporcionan excelentes soluciones a sistemas de matrices dispersas para problemas de gran escala, proporcionando soluciones de mayor precisión con menor consumo de memoria. Esto hace que estas técnicas sean altamente adecuadas para casos de uso en ingeniería.

Programación Lineal y Sus Aplicaciones en Ingeniería y Economía  

La Programación Lineal (PL) es un método indispensable para optimizar (maximizar o minimizar) funciones objetivo lineales sujetas a restricciones. Un problema básico de programación lineal típicamente toma la forma de una fórmula explícita:

\(\begin{aligned} \text{Objective:} & \quad \min_{x} \; c^T x, \\ \text{Constraints:} & \quad Ax \leq b,\\ & \quad x \geq 0, \end{aligned}\)

donde \(c\) representa el vector de coeficientes de una función objetivo, \(A\) representa una matriz de restricciones, \(b\) representa el vector constante y \(x\) denota el vector de variables de decisión. Los modelos de programación lineal permiten a los tomadores de decisiones encontrar soluciones óptimas bajo restricciones de recursos limitados abstractando problemas del mundo real en modelos de programación lineal y encontrando soluciones óptimas bajo estas limitaciones de recursos limitados.

La programación lineal económica tiene muchos usos prácticos en optimizar carteras de inversión, controlar costos y desarrollar modelos de equilibrio del mercado. Un método clásico para resolver problemas de programación lineal - conocido como el método simplex - se mueve iterativamente de vértice en vértice en busca de la optimalidad usando soluciones básicas de sistemas lineales como base para crear un tableau simplex hasta que todas las condiciones de optimalidad se hayan cumplido. Los solucionadores modernos frecuentemente combinan métodos de puntos interiores en este enfoque de solución para satisfacer las demandas computacionales planteadas por problemas más grandes.

El álgebra lineal numérica y aplicada proporciona algoritmos numéricos eficientes, soporte teórico y soluciones prácticas para problemas de optimización en ingeniería y economía. Desde resolver sistemas lineales de gran escala hasta la optimización de producción y regulación del mercado, estas metodologías demuestran su valor con alto valor práctico y prometedoras perspectivas de aplicación.

Aplicaciones Interdisciplinarias del Álgebra Lineal

Aplicaciones en Aprendizaje Automático y Ciencia de Datos  

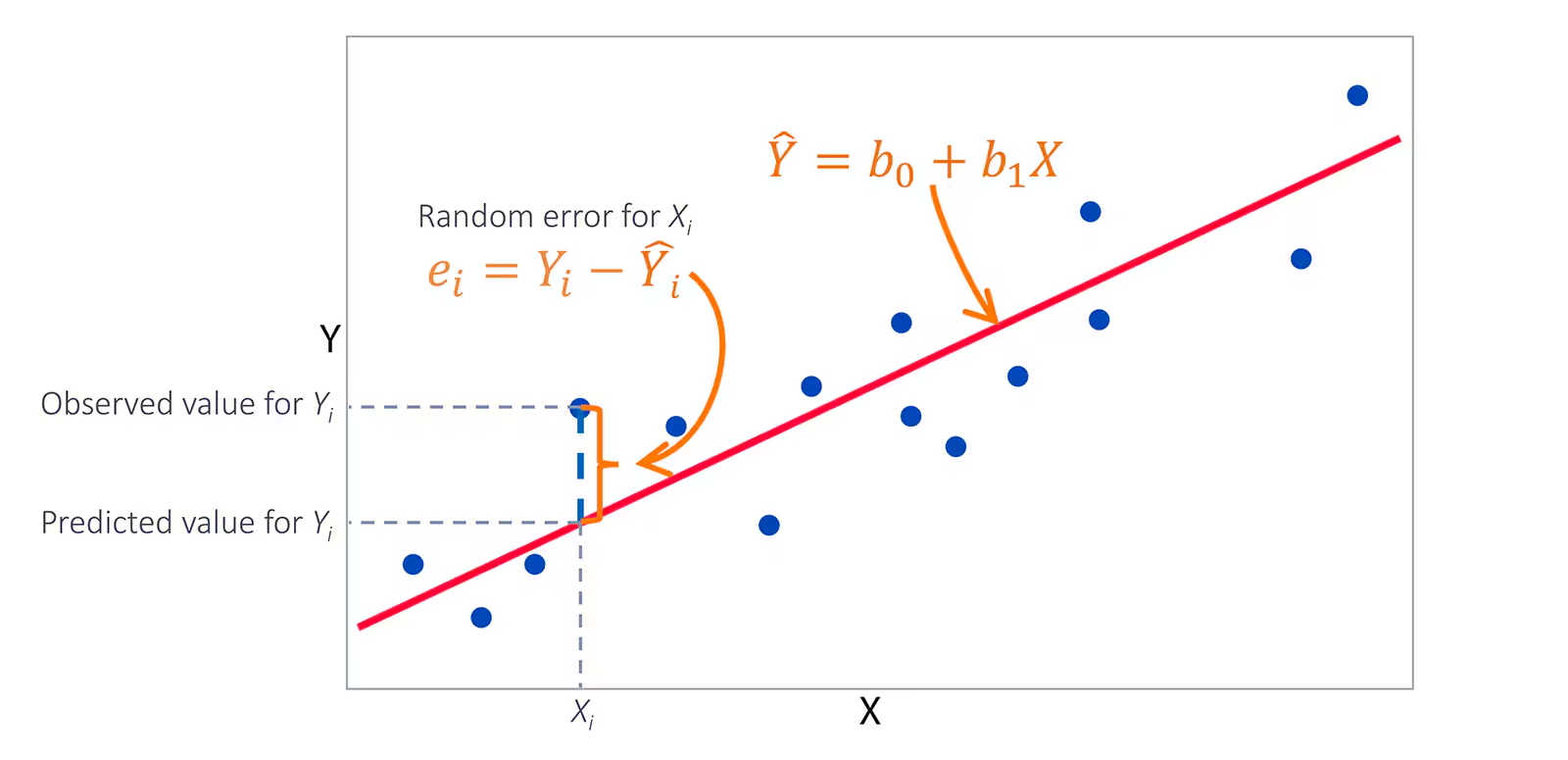
El álgebra lineal ha sido considerada durante mucho tiempo una base teórica indispensable en el aprendizaje automático y la ciencia de datos, sirviendo como columna vertebral para numerosos modelos de aprendizaje automático construidos sobre operaciones matriciales y teoría del espacio vectorial. Al resolver regresión lineal utilizando métodos de regresión de mínimos cuadrados, como el Método de Mínimos Cuadrados u otras estrategias de optimización, a menudo necesitamos abordar desafíos de optimización como:

\(\min_{w}\|Xw-y\|_2^2,\)  

Donde \(X\) representa una matriz de características de muestra, \(w\) representa un vector de pesos desconocidos por determinar y \(y\) se refiere a una variable objetivo. Para resolverlo a través de ecuaciones normales.

\(X^TXw=X^Ty,\)  

La solución analítica se puede expresar como  

\(w=(X^TX)^{-1}X^Ty,\)  

Un enfoque efectivo para la estimación de parámetros implica emplear técnicas de inversión y multiplicación de matrices para la estimación de parámetros.

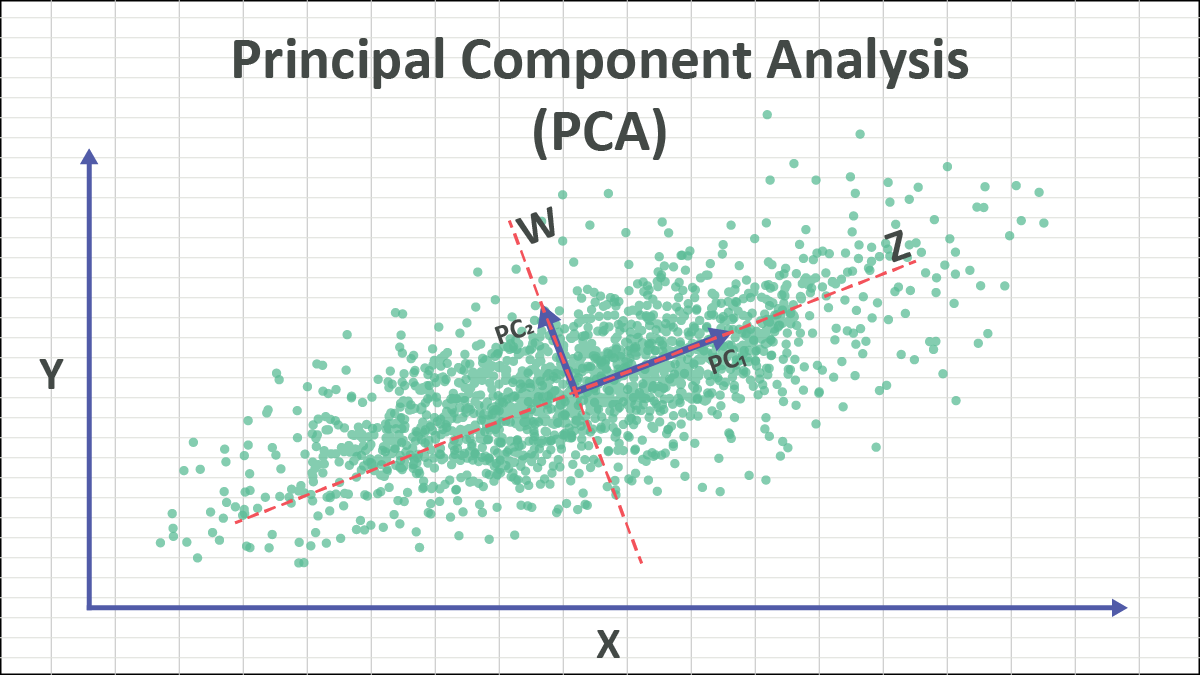
El Análisis de Componentes Principales (PCA), usado para la reducción de dimensionalidad de datos, extrae los componentes más esenciales realizando una descomposición de valores propios en su matriz de covarianza. Si asumimos \(X\), con todas sus filas asumidas centradas, entonces su matriz de covarianza está dada por  

\(C=\frac{1}{n-1}X^TX.\)  

Al resolver el problema de valores y vectores propios para \(C\), se puede seleccionar \(k\) vectores propios más grandes como bases de proyección para lograr tanto reducción de dimensión como compresión de datos. La descomposición en valores singulares (SVD) juega un papel integral en los sistemas de recomendación, procesamiento de imágenes y minería de textos; sus fórmulas de descomposición se dan aquí:

\(A=U\Sigma V^T,\)  

Las herramientas de modelado de datos ofrecen una poderosa solución para comprender las estructuras de datos.

Los cálculos de gradiente utilizados al entrenar redes neuronales o modelos complejos dependen en gran medida del cálculo matricial. La propagación hacia adelante y hacia atrás entre capas implica esencialmente multiplicaciones de matrices y operaciones derivadas; por ejemplo, en una red neuronal simple de avance, el cálculo podría representarse como:

\(y=f(Wx+b),\)  

Donde \(f\) representa una función de activación y \(W\) y \(b\) representan la matriz de pesos y el vector de sesgo, respectivamente, vectorizar operaciones permite no solo usar la aceleración de hardware de manera más eficiente, sino también simplificar los procesos de diferenciación de modelos multicapa de manera más fluida.

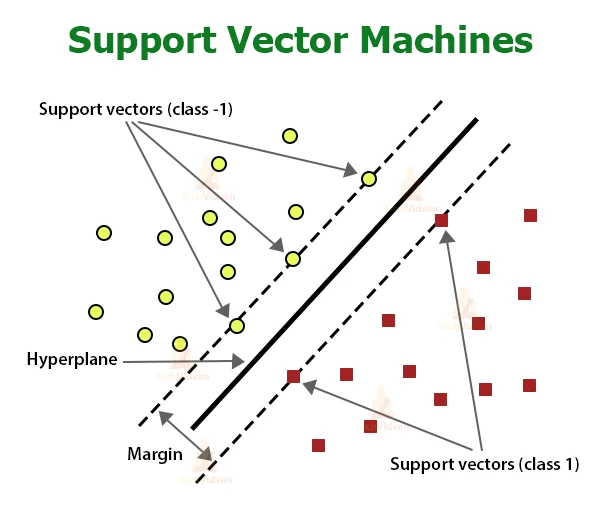
Las máquinas de soporte vectorial, los algoritmos de agrupamiento (como K-means) y las operaciones de convolución en reconocimiento de imágenes dependen en gran medida de la teoría del álgebra lineal para propósitos de soporte y cálculo. Las herramientas y métodos de álgebra lineal ofrecen a los científicos de datos y expertos en aprendizaje automático un invaluable soporte teórico y marco computacional al gestionar grandes volúmenes de datos o crear algoritmos eficientes.

Este artículo proporcionó una introducción al álgebra lineal, operaciones matriciales, algoritmos numéricos y sus aplicaciones interdisciplinarias a través de ejemplos y fórmulas. A través de ellos, demostró cómo esta disciplina ofrece un gran valor práctico en modelado de ingeniería, optimización económica y ciencia de datos - inspirando pensamiento innovador mientras se resuelven problemas del mundo real y avanzando en el desarrollo futuro.

referencias:

https://en.wikipedia.org/wiki/Linear_algebra

https://en.wikipedia.org/wiki/QR_decomposition

https://en.wikipedia.org/wiki/Singular_value_decomposition